字数

1006 字

阅读时间

5 分钟

奇零偶倍

$${\int }_{-a}^{a}f(x)dx=\{\begin{array}{ll}0& f(x)\text{为奇函数}\\ 2{\int }_0^{a}f(x)dx& f(x)\text{为偶函数}\end{array}$$

交换

$${\int }_0^{\frac{\pi }{2}}f(\sin x,\cos x)dx={\int }_0^{\frac{\pi }{2}}f(\cos x,\sin x)dx$$

推论一

$${\int }_0^{\frac{\pi }{2}}{\sin }^{n}xdx={\int }_0^{\frac{\pi }{2}}{\cos }^{n}xdx=\{\begin{array}{ll}\frac{(n-1)!!}{n!!}& n\text{ 为奇 }\\ \frac{(n-1)!!}{n!!}\cdot \frac{\pi }{2}& n\text{ 为偶 }\end{array}$$

推论二

$${\int }_0^{\frac{\pi }{2}}f(\sin x)dx={\int }_0^{\frac{\pi }{2}}f(\cos x)dx$$

例题

$$\text{求}{\int }_0^{\frac{\pi }{2}}\frac{{\sin }^{2020}x}{{\sin }^{2020}x+{\cos }^{2020}x}dx$$

具体过程如下：

$$\begin{array}{rl}& {\int }_0^{\frac{\pi }{2}}\frac{{\sin }^{2020}x}{{\sin }^{2020}x+{\cos }^{2020}x}dx\text{(1)}\\ & {\int }_0^{\frac{\pi }{2}}\frac{{\cos }^{2020}x}{{\sin }^{2020}x+{\cos }^{2020}x}dx\text{(2)}\\ \\ & \text{根据性质可得一式和二式相等。}\\ \\ & {\int }_0^{\frac{\pi }{2}}\frac{{\sin }^{2020}x}{{\sin }^{2020}x+{\cos }^{2020}x}dx={\int }_0^{\frac{\pi }{2}}\frac{{\cos }^{2020}x}{{\sin }^{2020}x+{\cos }^{2020}x}dx\\ \\ & \text{所以可以得到原式等于}\frac{1}{2}(\text{一式}+\text{二式})\\ \\ & {\int }_0^{\frac{\pi }{2}}\frac{{\sin }^{2020}x}{{\sin }^{2020}x+{\cos }^{2020}x}dx=\frac{1}{2}{\int }_0^{\frac{\pi }{2}}1dx=\frac{\pi }{4}\end{array}$$

再来一个例题：

$${\int }_0^{\frac{\pi }{2}}{\sin }^3(x)dx=\frac{2!!}{3!!}=\frac{2\times 1}{3\times 1}=\frac{2}{3}$$

换限

$${\int }_0^{\pi }f(\sin x)dx=2\cdot {\int }_0^{\frac{\pi }{2}}f(\sin x)dx$$

举个例子：

$${\int }_0^{\pi }{\sin }^{6}xdx=2{\int }_0^{\frac{\pi }{2}}{\sin }^{6}xdx=2\cdot \frac{5!!}{6!!}\cdot \frac{\pi }{2}$$

$xf(x)$ 的变换

$${\int }_0^{\pi }x\cdot f(\sin x)dx=\frac{\pi }{2}{\int }_0^{\pi }f(\sin x)dx$$

举个例子：

$${\int }_0^{\pi }x\cdot {\sin }^{5}xdx=\frac{\pi }{2}{\int }_0^{\pi }{\sin }^{5}xdx=\frac{\pi }{2}\cdot 2\cdot {\int }_0^{\frac{\pi }{2}}{\sin }^{5}xdx=\frac{\pi }{2}\cdot 2\cdot \frac{4!!}{5!!}$$

周期为 T 的函数

一、

$${\int }_a^{a+T}f(x)dx={\int }_0^{T}f(x)dx={\int }_{-\frac{T}{2}}^{\frac{T}{2}}f(x)dx$$

二、

$${\int }_a^{a+nT}f(x)dx=n\cdot {\int }_0^{T}f(x)dx=n\cdot {\int }_{-\frac{T}{2}}^{\frac{T}{2}}f(x)dx$$

反常积分中的伽马函数

伽马函数一般用来快速计算反常积分（广义积分）

其核心是：

$$\mathrm{\Gamma }(n)={\int }_0^{+\mathrm{\infty }}{x}^{n-1}{e}^{-x}dx(n>0)$$

IMPORTANT

注意，关于伽马函数，一般题目都是需要换元的，也就是需要凑出伽马函数的形式，然后再计算。

而伽马函数形式的核心在于 $e^{-x}$ ，也就是需要将题目中的这一项换成 $e^{-x}$ 形式，才能继续后面的计算。

其中，伽马函数具备以下这样的递推关系：

$$\mathrm{\Gamma }(n+1)=n\mathrm{\Gamma }(n)$$

特别的是：

$$\mathrm{\Gamma }(n+1)=n!\text{当}n\text{为自然数的时候}$$

除此之外，伽马函数还有以下性质：

$$\mathrm{\Gamma }(1)=1$$$$\mathrm{\Gamma }(\frac{1}{2})=\sqrt{\pi }$$

半整数阶公式：

$$\mathrm{\Gamma }(n+\frac{1}{2})=\frac{(2n)!}{4^{n}n!}\sqrt{\pi }$$

举例使用

当遇到形如 ${\int }_0^{+\mathrm{\infty }}{x}^k{e}^{-ax}dx$ 的积分时，可通过变量替换转化为伽马函数形式。

通用步骤：

1. 变量替换：令 $t=ax$ ，则 $x=\frac{t}{a}$ ， $dx=\frac{1}{a}dt$
2. 代入积分：$${\int }_0^{+\mathrm{\infty }}{\left(\frac{t}{a}\right)}^k{e}^{-t}\cdot \frac{1}{a}dt=\frac{1}{a^{k+1}}{\int }_0^{+\mathrm{\infty }}{t}^k{e}^{-t}dt=\frac{\mathrm{\Gamma }(k+1)}{a^{k+1}}$$
3. 化简结果：利用 $\mathrm{\Gamma }(k+1)=k!$ （若 $k$ 为自然数），或保留伽马函数形式

例题

计算

$${\int }_0^{+\mathrm{\infty }}\sqrt{x}{e}^{-x^2}dx$$

令 $t=x^2$ ，则 $x=\sqrt{t}$ ， $dx=\frac{1}{2}{t}^{-\frac{1}{2}}dt$

则积分变为：

$${\int }_0^{+\mathrm{\infty }}{t}^{\frac{1}{4}}{e}^{-t}\cdot \frac{1}{2}{t}^{-\frac{1}{2}}dt=\frac{1}{2}{\int }_0^{+\mathrm{\infty }}{t}^{-\frac{1}{4}}{e}^{-t}dt=\frac{1}{2}\mathrm{\Gamma }(\frac{3}{4})$$

定积分中的贝塔函数

贝塔函数的定义是：

$$B(p,q)={\int }_0^1{x}^{p-1}(1-x{)}^{q-1}dx(p>0,q>0)$$

性质

对称性：

$$B(p,q)=B(q,p)$$

特殊值：

$$B(1,1)=1$$$$B(\frac{1}{2},\frac{1}{2})=\pi$$

与伽马函数之间的关系

$$B(p,q)=\frac{\mathrm{\Gamma }(p)\mathrm{\Gamma }(q)}{\mathrm{\Gamma }(p+q)}$$

适用场景

适合用于处理 $0$ 到 $1$ 上的积分，形如： ${\int }_0^1{x}^a(1-x{)}^{b}dx$

以及通过变量替换可以换到 $0$ 到 $1$ 上的积分。

例如：

$${\int }_0^{+\mathrm{\infty }}\frac{x^k}{(1+x{)}^m}dx$$

来个例题：

$${\int }_0^{+\mathrm{\infty }}\frac{x^3}{(1+x{)}^5}dx$$

按照之前的做法是要拆项裂项。

这里需要进行换元计算： 令 $t=\frac{x}{1+x}$ ，则 $x=\frac{t}{1-t}$ ， $dx=\frac{1}{(1-t{)}^2}dt$

积分变换为：

$${\int }_0^1{\left(\frac{t}{1-t}\right)}^3\cdot \frac{1}{(1-t{)}^{-5}}\cdot \frac{1}{(1-t{)}^2}={\int }_0^1{t}^3(1-t{)}^{0}dt=B(4,1)$$

然后再利用贝塔函数和伽马函数之间的关系进行计算，得到最后的结果。

再来一个例题：

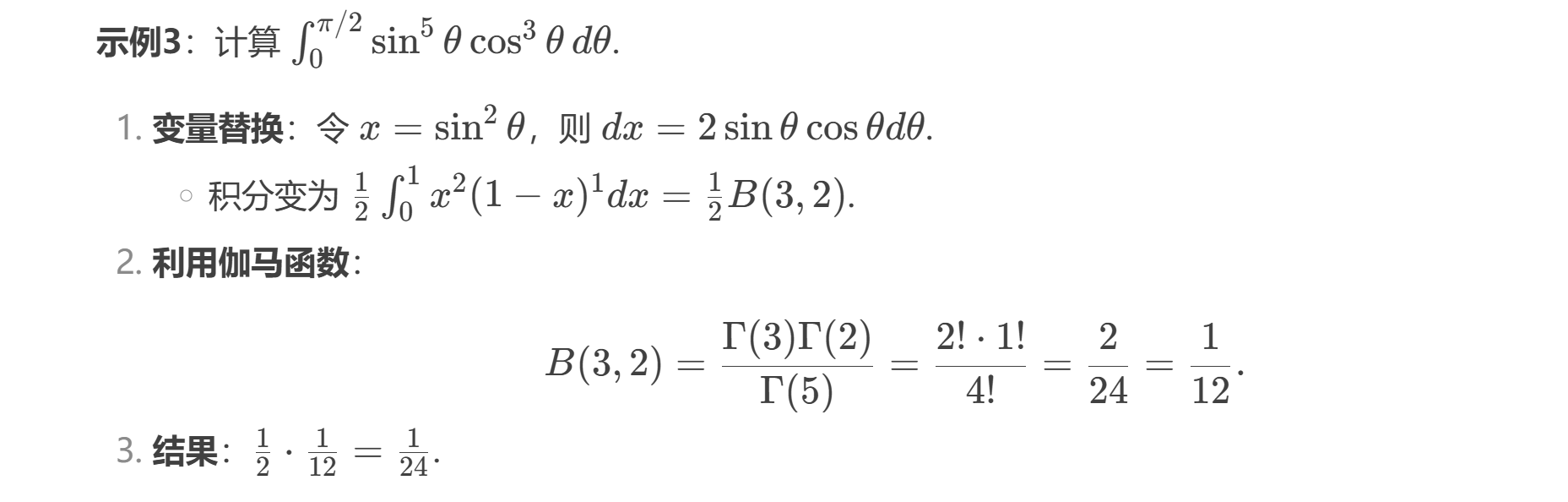
NOTE

具体问题具体分析，适用贝塔函数不见得是最简单的方法，比如示例 3，直接可以点火公式得到最后的结果。

前面一道题也是，直接就可以得到最后的结果，不需要再去硬凑贝塔函数的形式。

贡献者

王海平

文件历史

最后编辑于 15 天前查看完整历史

b8e1c-update