字数

1659 字

阅读时间

8 分钟

基本积分公式 (需要记忆)

$$\begin{array}{c}\int k\mathrm{d}x=kx+C\\ \int x^n\mathrm{d}x=\frac{x^{n+1}}{n+1}+C(n\ne -1)\\ \int \frac{1}{x}\mathrm{d}x=\ln |x|+C\\ \int e^x\mathrm{d}x=e^x+C\\ \int a^x\mathrm{d}x=\frac{a^x}{\ln a}+C\\ \int \frac{1}{a^2+x^2}\mathrm{d}x=\frac{1}{a}\arctan \frac{x}{a}+C-\text{arccot}\frac{x}{a}+C\\ \int \frac{1}{x^2-a^2}\mathrm{d}x=\frac{1}{2a}\ln |\frac{x-a}{x+a}|+C\\ \int \frac{dx}{a^2-x^2}=\frac{1}{2a}\ln \left|\frac{x+a}{x-a}\right|+C\\ \\ \\ \\ \int \frac{\mathrm{d}x}{\sqrt{x^2+a^2}}=\ln (x+\sqrt{x^2+a^2})+C\\ \int \frac{\mathrm{d}x}{\sqrt{x^2-a^2}}=\ln |x+\sqrt{x^2-a^2}|+C\\ \int \frac{1}{\sqrt{a^2-x^2}}\mathrm{d}x=\arcsin \frac{x}{a}+C=-\arccos \frac{x}{a}+C\end{array}$$$$\begin{array}{c}\int \cos x\mathrm{d}x=\sin x+C\\ \int \sin x\mathrm{d}x=-\cos x+C\\ \int \sec x\mathrm{d}x=\ln |\sec x+\tan x|+C\\ \int \csc x\mathrm{d}x=\ln |\csc x-\cot x|+C\\ \int \sec x\tan x\mathrm{d}x=\sec x+C\\ \int \csc x\cot x\mathrm{d}x=-\csc x+C\\ \int \tan x\mathrm{d}x=\ln |\sec x|+C\\ \int {\sec }^{2}x\mathrm{d}x=\tan x+C\\ \int {\csc }^{2}x\mathrm{d}x=-\cot x+C\end{array}$$

通过做题发现， $\int {\sec }^{2}x\mathrm{d}x=\tan x+C$ 使用的次数比较多。

同时一般会去配 $\frac{1}{{\cos }^{2}x}$

由此可以得到

$$\int \frac{1}{{\cos }^{2}x}dx=\int {\sec }^{2}xdx=\tan x+C$$

除此之外，还需要知道的是：

$${\tan }^2+1={\sec }^{2}x$$

有理函数的不定积分

多项式的商，一般称为有理函数。

同时，这里的多项式分为真分式、假分式。

$\frac{x+1}{x^2-5x+6}$ 就是真分式，而 $\frac{x^2+1}{x^2-5x+6}$ 和 $\frac{2x^4+x^2+3}{x^2+1}$ 则是假分式。

综上，我们将判读的方法进行总结：

IMPORTANT

分母的最高次幂大于分子的最高次幂，则称为真分式

分母的最高次幂小于等于分子的最高次幂，则称为假分式

在进行积分的过程中，要把假分式变换为真分式。

分母能拆项列项

先是分子最高次幂大于分母最高次幂：

例如：

$$\frac{2x^4+x^2+3}{x^2+1}$$

这个很明显是个假分式，我们要将其拆出来，出现真分式。

这里用到的方法是用分子除以分母。

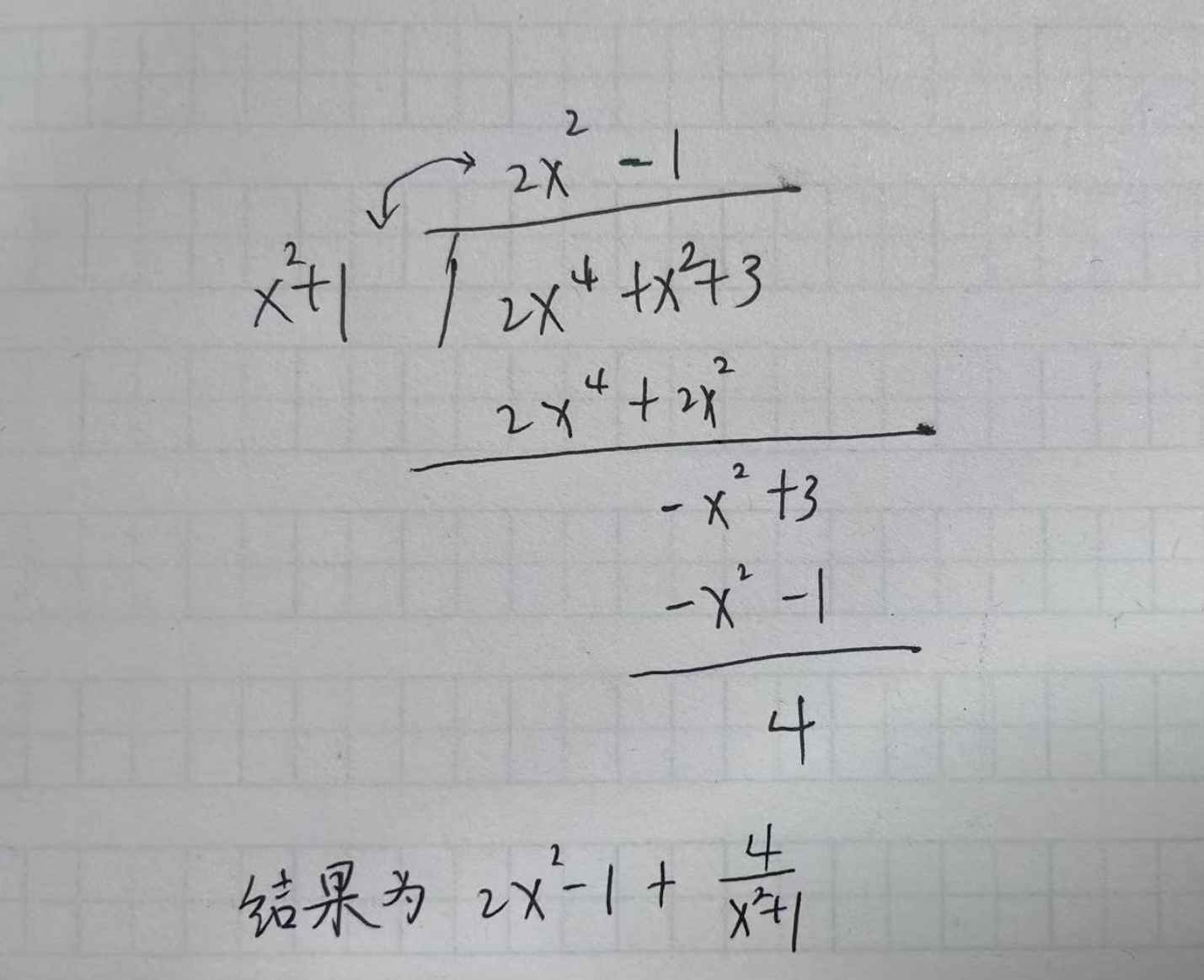
通过上面这种除法，可以得到最后的结果：

$$2x^2-1+\frac{4}{x^2+1}$$

然后再进行计算，这里指的是已经化成了真分式之后的计算。

再就是针对复杂题目：

$$\frac{x^5-1000}{(x+1{)}^2(x-1{)}^3(x^2+1{)}^4}$$

这就需要进行拆项列项

IMPORTANT

拆项列项是有前提的：

前提是分母已经分解到不能分解了

注意看：

我们将原式拆解为：

$$\frac{}{x+1}+\frac{}{(x+1{)}^2}+\frac{}{(x-1)}+\frac{}{(x-1{)}^2}+\frac{}{(x-1{)}^3}+\frac{}{x^2+1}+\frac{}{(x^2+1{)}^2}+\frac{}{(x^2+1{)}^3}+\frac{}{(x^2+1{)}^4}$$

观察上式：

分母要拆成如下形式：

$$(x+1{)}^2\text{要拆成}\frac{}{(x+1)}+\frac{}{(x+1{)}^2}\cdots$$

然后是分子，分子要拆成：

分子的最高次幂比分母的核心部分低一次。

比如，前两项，核心部分是 $(x+1)$ ，次数是 $1$ ，所以，比其低一次是常数。

可以得到：

$$\frac{A}{x+1}+\frac{B}{(x+1{)}^2}$$

然后看接下来的三项，其核心部分是 $(x-1)$ ，比其低一次，结果是常数。

所以得到：

$$\frac{C}{x-1}+\frac{D}{(x-1{)}^2}+\frac{E}{(x-1{)}^3}$$

再来看最后面四项，其核心部分是 $x^2+1$ ，最高次数为 $2$ ，而分子要比其低一次幂，所以，要设为 $Ax+B$

所以可以得到：

$$\frac{A_{1}x+B_1}{x^2+1}+\frac{A_{2}x+B_2}{(x^2+1{)}^2}+\frac{A_{3}x+B_3}{(x^2+1{)}^3}+\frac{A_{4}x+B_4}{(x^2+1{)}^4}$$

然后在是一个一个去求解，很麻烦，但是上面这个题目考试不会考的。

NOTE

这里有一个方法，是在信号与系统中的留数法，这个方法简单说是"盖起来算其他" 但是这个方法只能用于分母最高次幂为 2 次的情况 当分母最高次幂为 2 次的时候，根据上面的方法进行拆解，得到的是两个项，而只能用于 2 次幂的哪个，低次幂的哪一项不能使用，具体计算方法在“留数法”下面的“一道难题”中有具体解答，需要注意的是，在信号与系统中可以讲 $j\omega$ 认为是 $x$ 。

IMPORTANT

以上方法只适用于：

1. 真分式，真分式才能拆项列项

2. 分母能够因式分解，且需要把它分解到不能再分解为止。

来几个例题。

例题

第一个

$$\int \frac{x+1}{x^2-5x+6}dx$$

先观察是不是真分式，很明显分母的最高次项大于分子的最高次项。

然后对分子进行拆项列项：

$$\Rightarrow \int \frac{A}{x-2}+\frac{B}{x-3}dx$$

然后需要通分计算得到 $A$ 、 $B$ 的值。

通过计算得到：

$$A=-3$$$$B=4$$

所以，原始可以换成：

$$\int \frac{-3}{x-2}+\frac{4}{x-3}dx$$

最后的结果是：

$$-3\ln |x-2|+4\ln |x-3|+C$$

第二个

$$\int \frac{x+2}{(2x+1)(x^2+x+1)}dx$$

很明显可以判断出这个是一个真分式

而字母也已经不能再因式分解了，所以我们有：

$$\Rightarrow \frac{x+2}{(2x+1)(x^2+x+1)}=\frac{A}{2x+1}+\frac{Bx+C}{x^2+x+1}$$

然后再就是通分求解。

可以得到：

$$A=2B=-1C=0$$

前面一部分是针对分母可以分开的情况：

分母不能拆项列项

如果出现分母不能分开的情况：

综上所述

NOTE

遇到有理函数的积分，无论是定积分还是不定积分。

先判断是不是真分式：

如果不是，利用"除法"去化成真分式形式

再判断分母是不是不能再因式分解（拆项裂项）：

如果不能再因式分解，则将分子给“凑”出来，凑成 $\int \frac{1}{x}dx$ 的形式，常数项部分分母进行配方

如果都可以，则进行拆项列项。

NOTE

如果不是真分式，

这里需要判断，首先是分子分母的最高次幂是否相等，如果相等，则需要提出来一个 “1”，剩余的部分则化为了真分式，再按照上面的方法进行计算。

如果分子的最高次幂大于分母的最高次幂，则需要进行 “除法”，用列竖式的方式用分母除以分子，得到一个结果以及一个余项，或者没有余项。

贡献者

王海平

文件历史

最后编辑于 14 天前查看完整历史

74726-vault backup: 2025-04-10 21:51:48