公式!
先来个大的:
其中,
当
上面这个公式将五个微妙且看似无关的数学符号 简直是太优美了。
验证
如何验证上面的公式是成立的呢?
最简单的方法就是直接将等式的左右两边直接泰勒展开即可。很轻松的就能得到相等。
但是这不是推导,具体的推导有点小复杂,文章来源。
在此之前,需要清楚欧拉公式的左右两边都可以看作是在描述在一个圆上的位置或者运动。
推导
假如说现在我们要用三角函数去描述圆心在复平面原点处的单位圆上的位置或者圆周运动轨迹,当圆弧角为
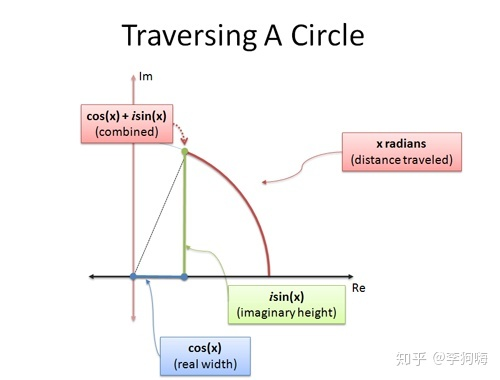
NOTE
数学中,复平面(英语:Complex plane)是用水平的实轴与垂直的虚轴建立起来的复数的几何表示。可视为一个具有特定代数结构**笛卡儿平面(实平面)**,一个复数的实部用沿着
在图中:
因此采用复数
上面的描述不难理解,可能不好理解的只是复平面的概念。
等式的右边解决完了,那么左边呢?左边是一个复指数,为什么就相等了呢?(由于欧拉公式等式左边复指数中的实部为零,只包含虚部,因此也可以称之为虚指数)
先举个实指数相关的例子,当看到
我们可以将
而通式就可以写为:
其中,
因此,跳开数值本身的大小问题,我们把“乘以实指数”看成是一种“增长”或者说是对初始值的一种“推动”作用(这里初始值是具有大小和方向属性的“复数”,复数包含实数和虚数,表达式可写为:复数 = 实部 +
再例如实数 ,可将其看做是:单位时间增长率为
这里先只考虑了增长率为实数时的增长作用,而以实数为增长率的这种“增长”或“推动”是沿着初始值方向进行的(复数可以看做是复平面上的矢量,因此具有方向属性)。
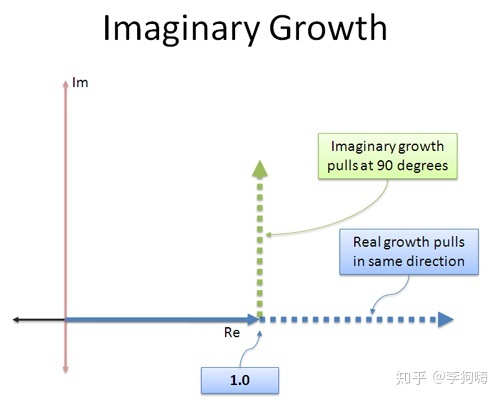
而虚指数所带来的增长作用就和实指数有所不同,虚指数的增长作用的方向与初始值的方向垂直,且随着数值的变化始终保持着这种垂直的关系,详情请见:《虚数i真的很“虚”吗?》。这种增长方式并不改变数的大小,而只改变复数的方向!例如,让任何数乘以虚数 ,都不会改变数的大小(或增长),而是改变数的方向。
在《自然底数e怎么就“自然”了?》中已经给出了自然底数
不够在上式中,我们假设的增长率为实数,但是,如果增长率为虚数呢?
其增长的示意图如下:
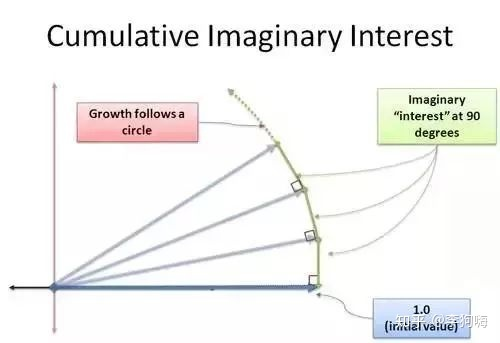
现在,“新的增长率”其实一直是沿着复数的垂直方向。并且这并不会改变复数的长度,但有人会提出质疑,因为上图所示的示意图是由一个个直角三角形组成,斜边当然比直角边更大。
但要知道,我们正在处理的是一个极限问题,当
最终将得到的结果是:复数长度(模长)不变的连续旋转。这是处理其与正弦、余弦之间关系的核心概念,当复数的增量始终与复数的方向保持垂直,得到的轨迹必将是一个圆!
下面用公式来证明这一点:
复数的模长为实部平方与虚部平方的和的平方根;转角为虚部除以实部的反正切值。
对于上式,如果
NOTE
模长增量:
最终模长:
转角增量:
最终转角:
如上式中
NOTE
模长增量:
最终模长:
转角增量:
最终转角:
即,将
那么当
NOTE
模长增量:
最终模长:
转角增量:
最终转角:
实际上就是复数
也就得到了
那对于更普遍的
NOTE
模长增量:
最终模长:
转角增量:
最终转角:
实际上也是复数
也就得到了
如果
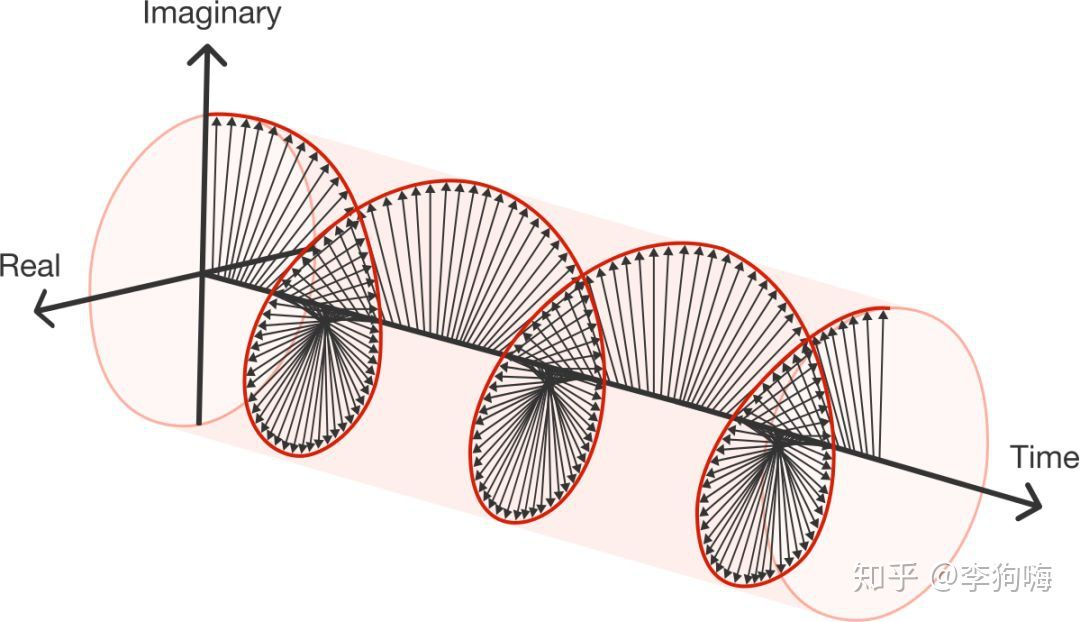
而这里只需要令
推导完成。
 王海平
王海平