字数

12797 字

阅读时间

51 分钟

监督学习

what is supervised learning

example:

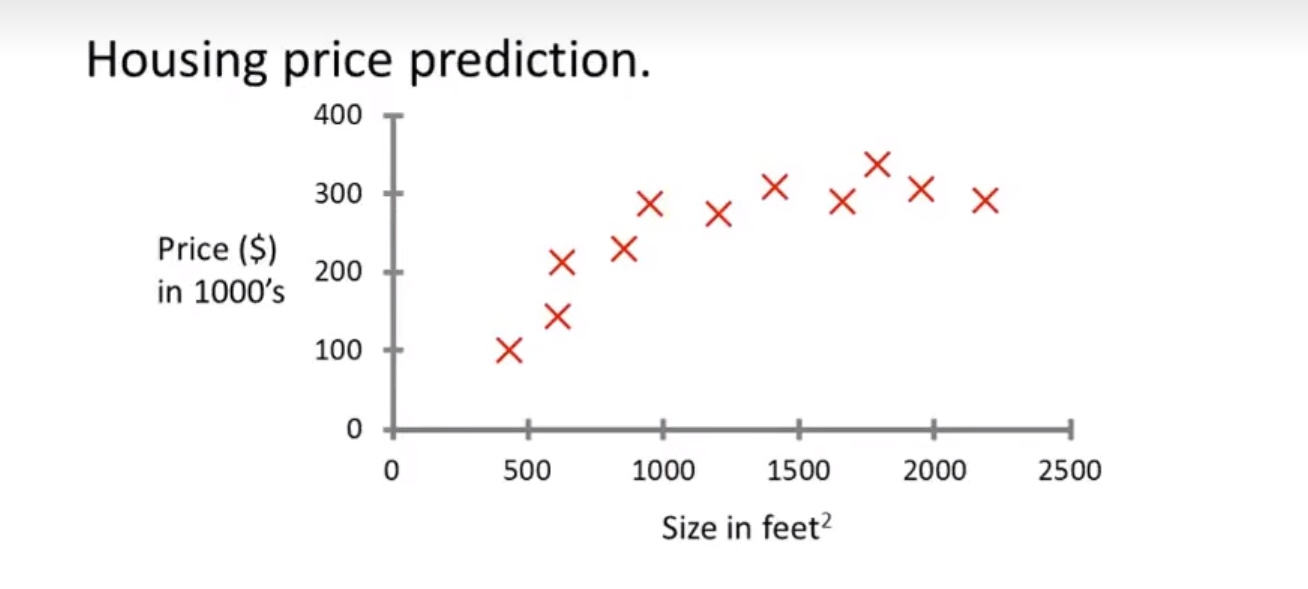
预测你想要的房子的房价是多少

可以用一条曲线来拟合数据，然后根据曲线来得到一个大概近似的数据。

问题在于是用什么样的模型来进行预测，可能是曲线也可能是直线

这样的问题也叫做 Regression Question 回归问题

我们想要预测连续的数值输出

other example：

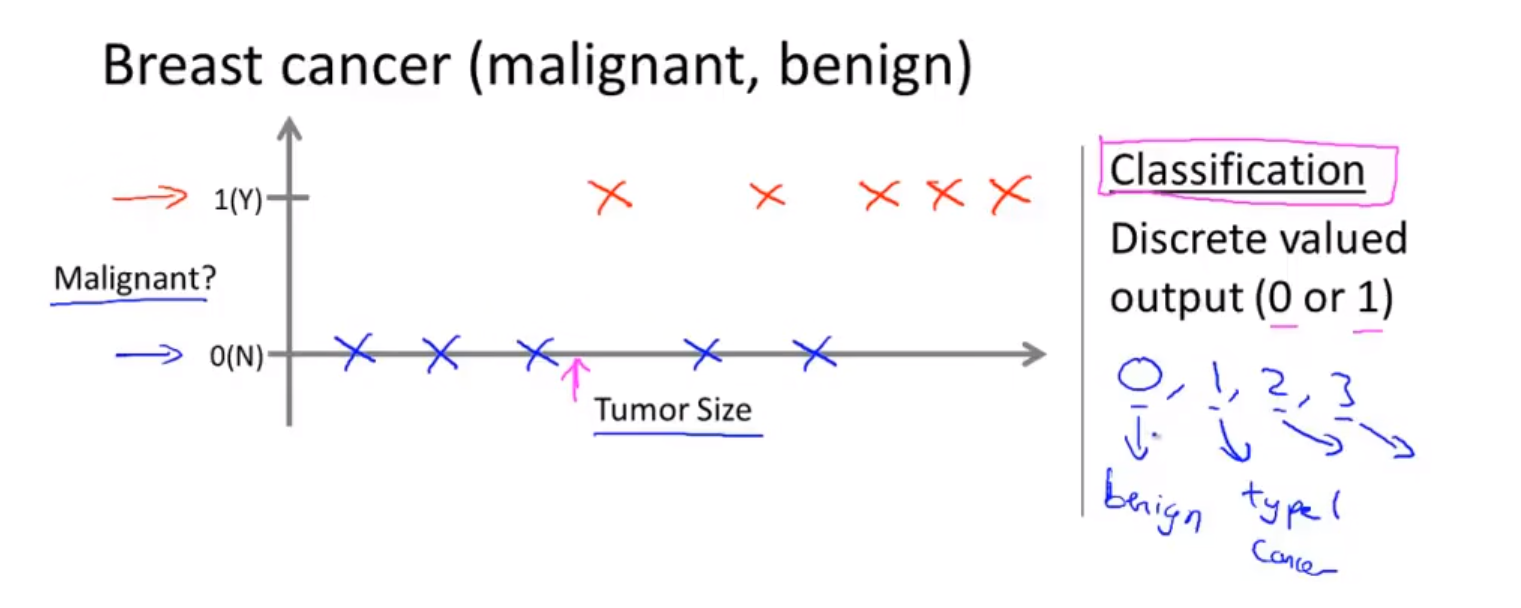
有关于肿瘤大小和是否是恶性肿瘤的预测（分类）

然后输入一个肿瘤的尺寸，然后得到肿瘤是良性的还是恶行的概率

这是一个分类问题（Classification Question）

我们设法预测一个离散值的输出 0 或者 1 恶性或者良性

在实际的例子中，可能会有多个类型的输出。

可能会设法预测离散值 0 1 2 3 ....

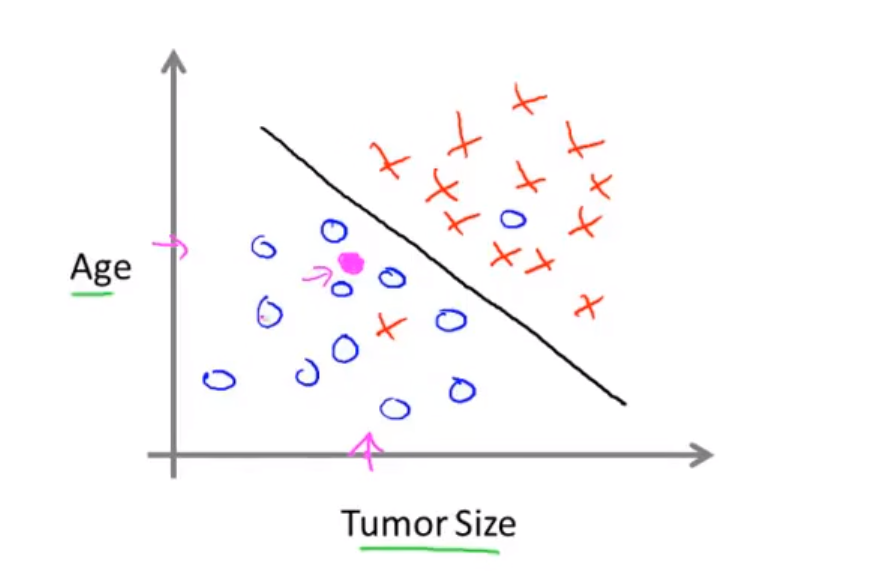
并且 我们还有可能将这样的分类问题划分到用一个维度上面去（二维到一维）就像上面那样。

方便我们去设置更多的特征（多个特征， 多个属性）

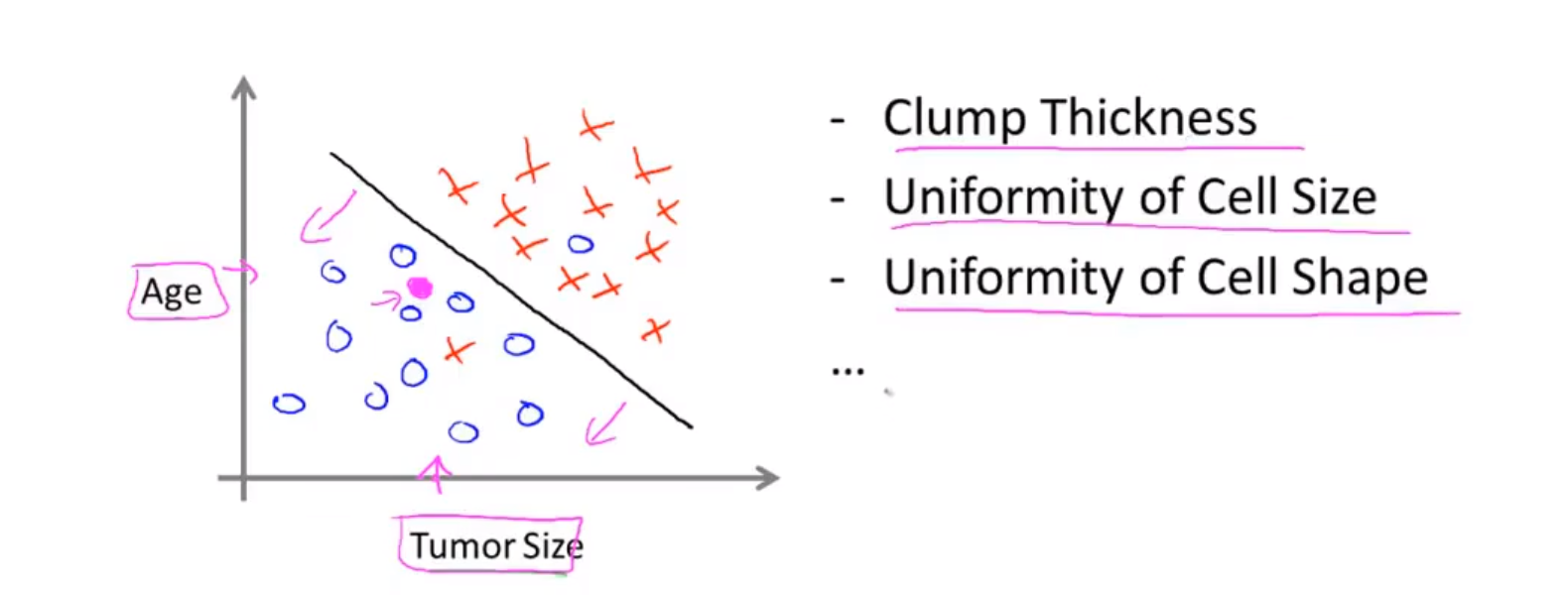
肿瘤大小、年龄、肿块厚度、瘤细胞均匀度、瘤细胞大小这五个特种

但是对于其他的学习任务，会涉及到无穷多个特征，

这个地方就需要用很多的属性或者特征或者线索来做预测。

如何处理无穷多的特征以及如何在计算机中存储无穷多的数量的事物

预测明天多少度就是一个回归问题。

总之有监督学习，就是一个具有标签的数据，进行分类或者回归

无监督学习

what is unsupervised learning

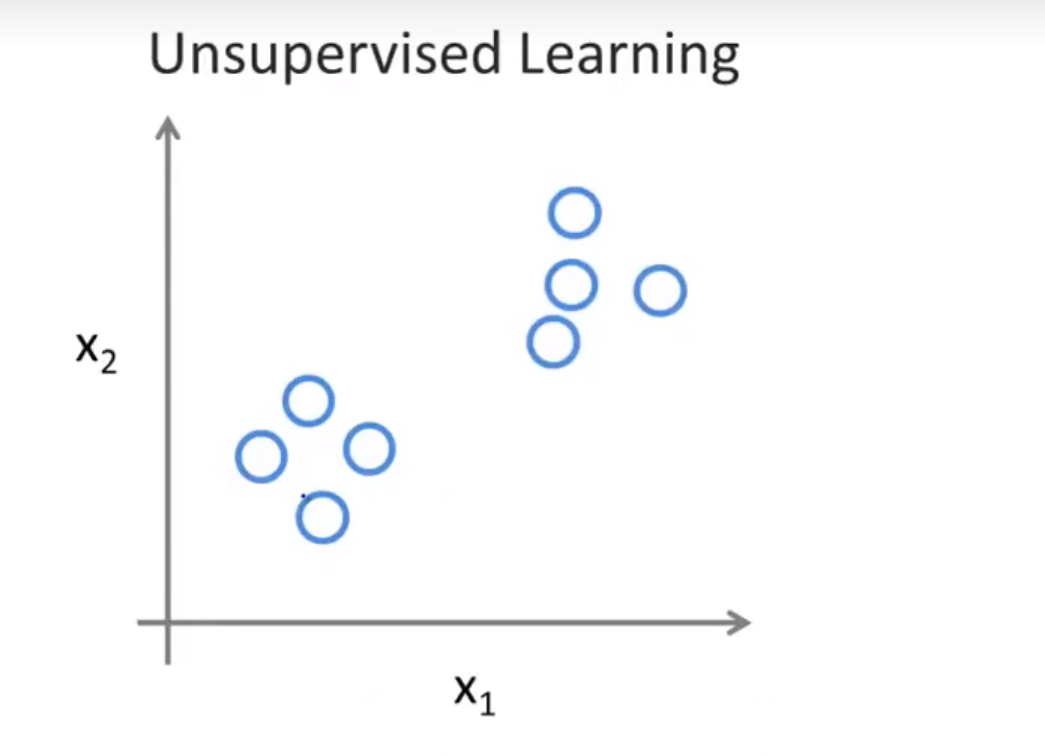会像是这样没有标签的样子

无监督学习算法可能会认为这个数据集中包含两个不同的簇

这样的分类就是聚类算法

可以看出来聚类算法是认为离得近的算作是一类。这里的离得近是广义上的离得近。

无监督学习算法可以认为其数据集是没有标签的（包括聚类算法）

（我们给出数据，计算机自己进行分类）

鸡尾酒会算法：

简单描述：在一个鸡尾酒会上，假设只有两个人进行同时讲话，同时又有两个麦克风进行录音，这两个麦克风距离两个人的距离是不一样的，所录的音中两个人的声音大小是不一样的，通过读取录音然后将重叠在一起的声音进行分离（the first output）让机器知道有不同的声音，并且进行分离

通过算法找出数据的结构

线性回归

form 监督学习supervisor learning

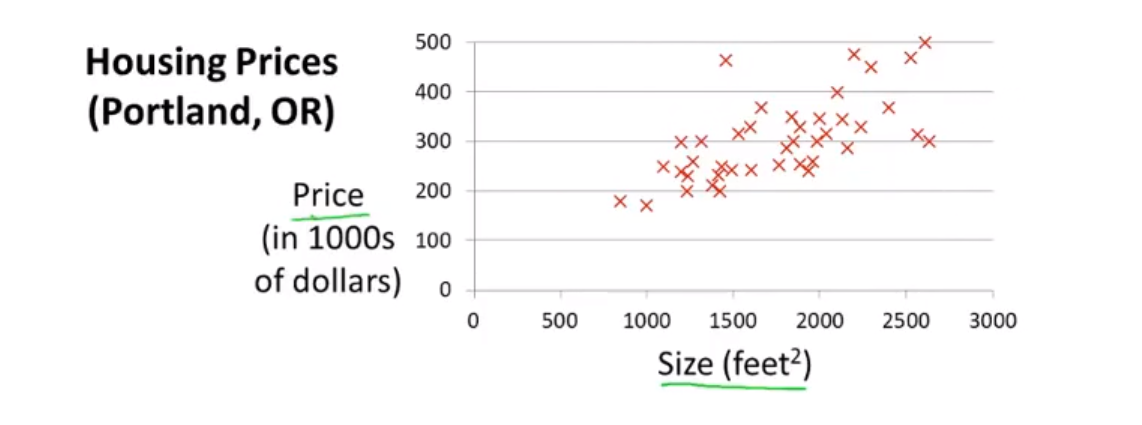
这是一个监督学习的例子。

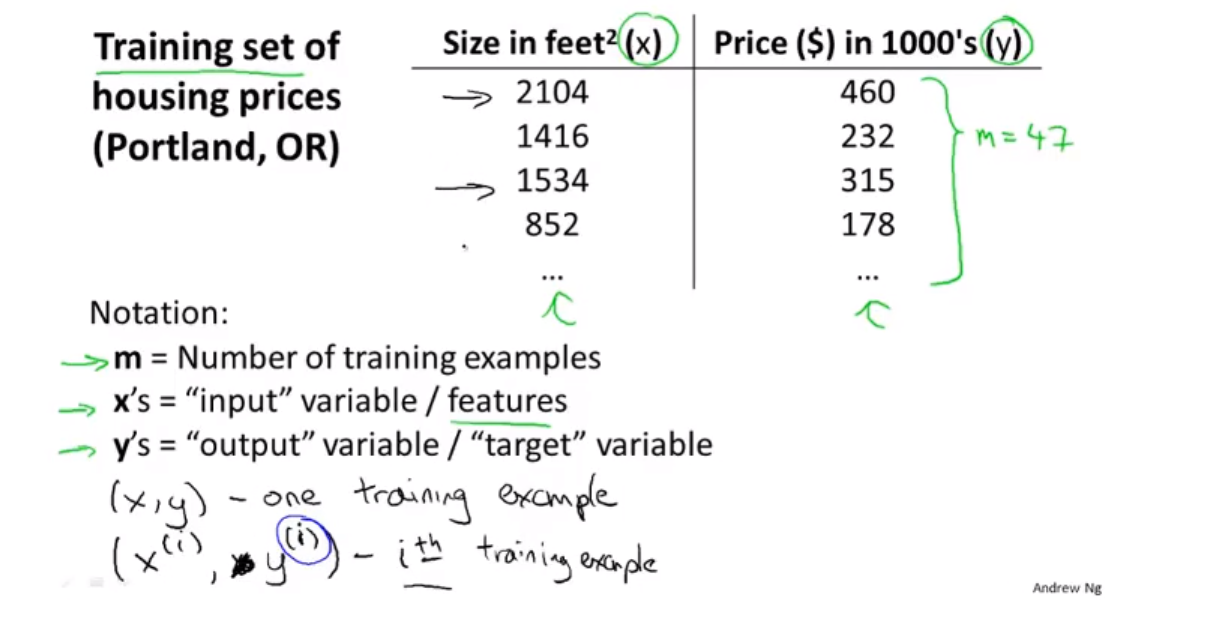
上面公式中的 ^(i) 代表是index ，指的是这个表格中的第 i 行 （训练集的一个索引）

下面是其大体的流程

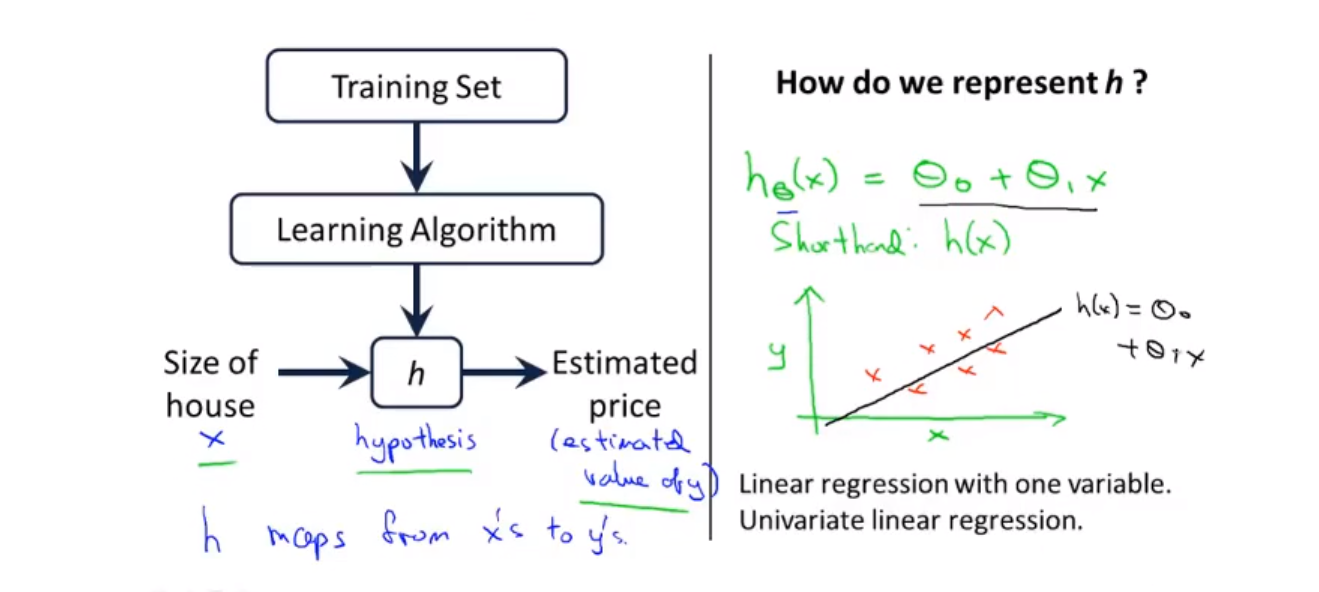
问题随之而来：

How to we represent h 怎么得到这个假设函数 h

像上图右侧这样进行假设这样一个 一元线性回归的函数

并且这也是一个单一变量的函数 （Univariate）

以上就是一个简单的线性回归（Linear regression）问题

代价函数

关于之前讲到的函数：h_\theta(x) = \theta_0 + \theta_1x

不同假设会得到不同的假设函数

$$\text{所以这个求最小化函数（solveminimize function）：}\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$$$\begin{gathered} \text{this }{h}_{\theta }(x^{(i)})\text{ is Compound function 复合函数} \\ \text{展开后是 }{h}_{\theta }(x)={\theta }_0+{\theta }_{1}x \end{gathered}$$

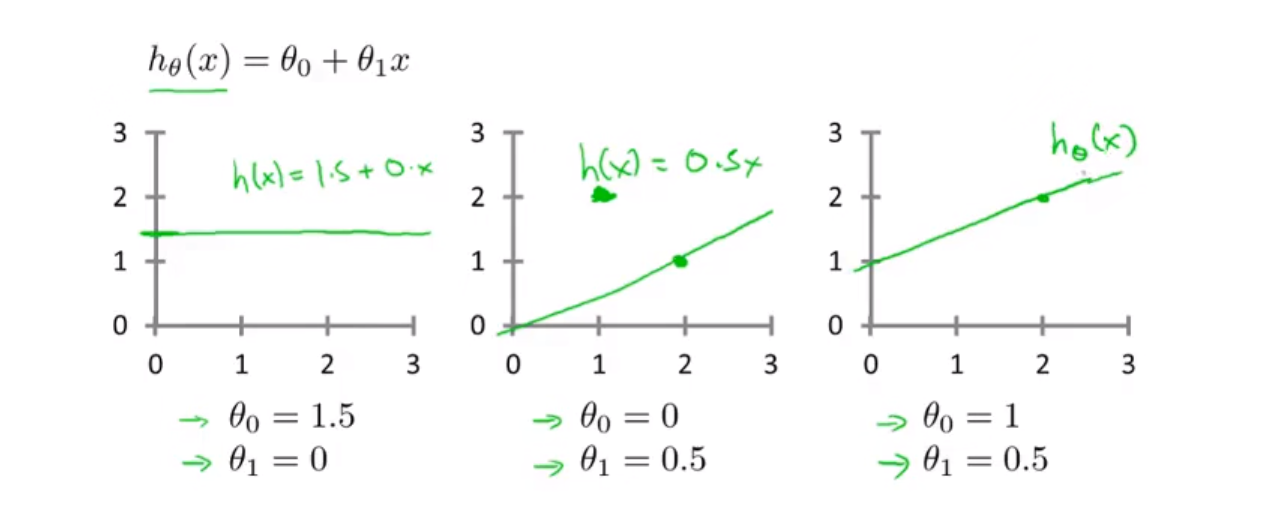
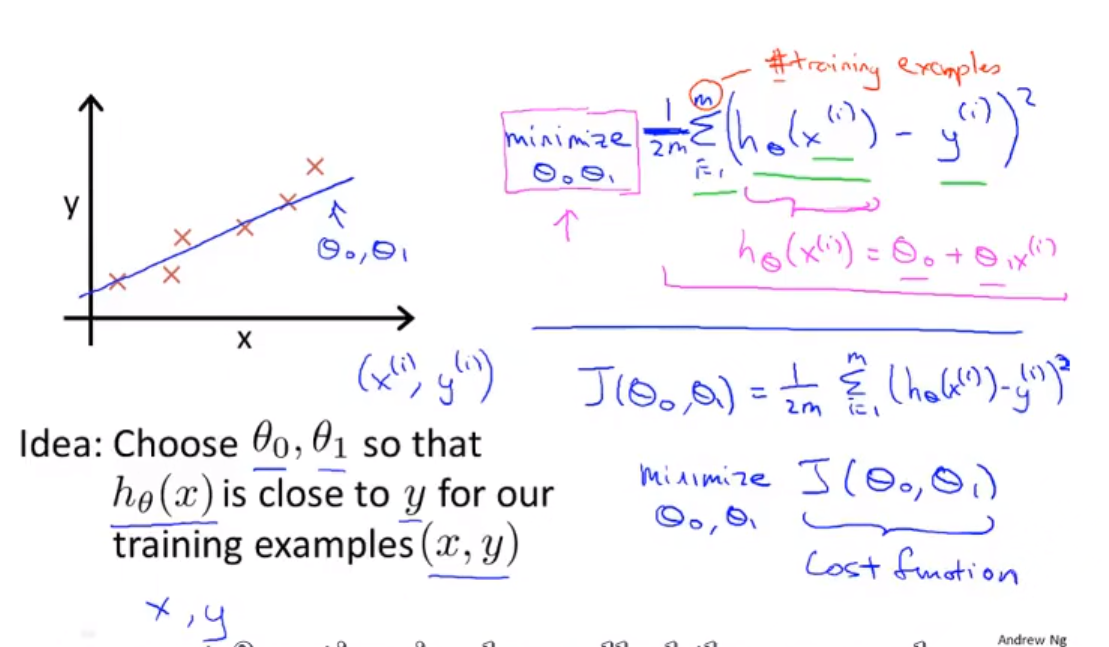
上面公式中 m 代表的是训练样本的个数

平方是为了放大大于1的误差和缩小小于1的误差，同时还消除了负号

描述出来就是 ： 各项差值平方的总和

上面这个函数就称为 代价函数，也被称为 平方误差函数

运用的原理就是 最小二乘法

解释：

$$\begin{gathered} \mathrm{表}\mathrm{函}\mathrm{数}=\sum (\mathrm{观}\mathrm{测}\mathrm{值}-\mathrm{理}\mathrm{论}\mathrm{值}{)}^2 \\ \mathrm{我}\mathrm{感}\mathrm{觉}\mathrm{反}\mathrm{过}\mathrm{来}\mathrm{也}\mathrm{是}\mathrm{成}\mathrm{立}\mathrm{的}。 \end{gathered}$$

---

所以 可以这么理解：

假设函数就是用来拟合实际数据的，代价函数就是这个假设函数与真是数据的接近程度

整体流程如下图

简化一下：

将 \theta_0 去掉 也就是相当于函数从原点出发。

$$h_{\theta }(X)\mathrm{就}\mathrm{是}\mathrm{预}\mathrm{设}\mathrm{出}\mathrm{来}\mathrm{的}\mathrm{函}\mathrm{数}J({\theta }_1)\mathrm{就}\mathrm{是}\mathrm{代}\mathrm{价}\mathrm{函}\mathrm{数}$$

---

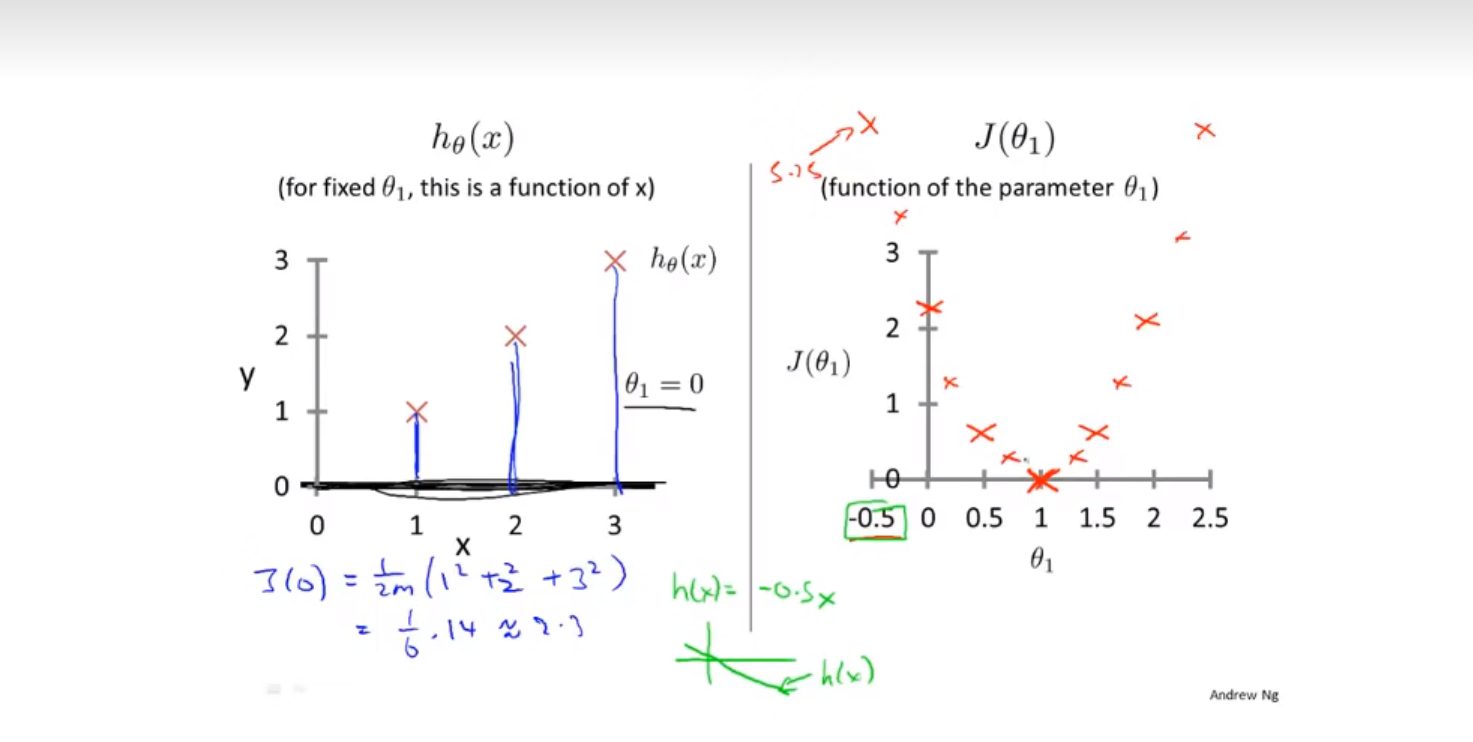
上面这个图的左半边代表的是根据不同的\theta_1绘制出来的预测函数的样子

右边这个图代表的是根据\theta_1的值绘制出来的代价函数的样子

还记得我们的目标吗？我们要让代价函数最小，在上图中，可以发现当\theta_1等于1的时候代价函数最小

而这个时候得到的\theta_1拟合出来的预测曲线是最贴近正确答案的

---

需要注意的是：

上面公式中 m 代表的是训练样本的个数

平方是为了放大大于1的误差和缩小小于1的误差，同时还消除了负号

$$h_{\theta }(x)={\theta }_{1}x$$

跟之前写的一样，就是观测值减去理论值的平方求和

根据之前的求最小化函数（代价函数），以及不断的变换\theta_1的值，就可以得到一条关于minimize的曲线，这样就能找到minimize（最小值)

---

针对之前的函数，我们的\theta_1会形成一个碗状函数，（blow shaped function）

那同样的，针对\theta_0同样的也会形成一个碗状函数（与训练集有关）。这样一来就形成了一个三维图像

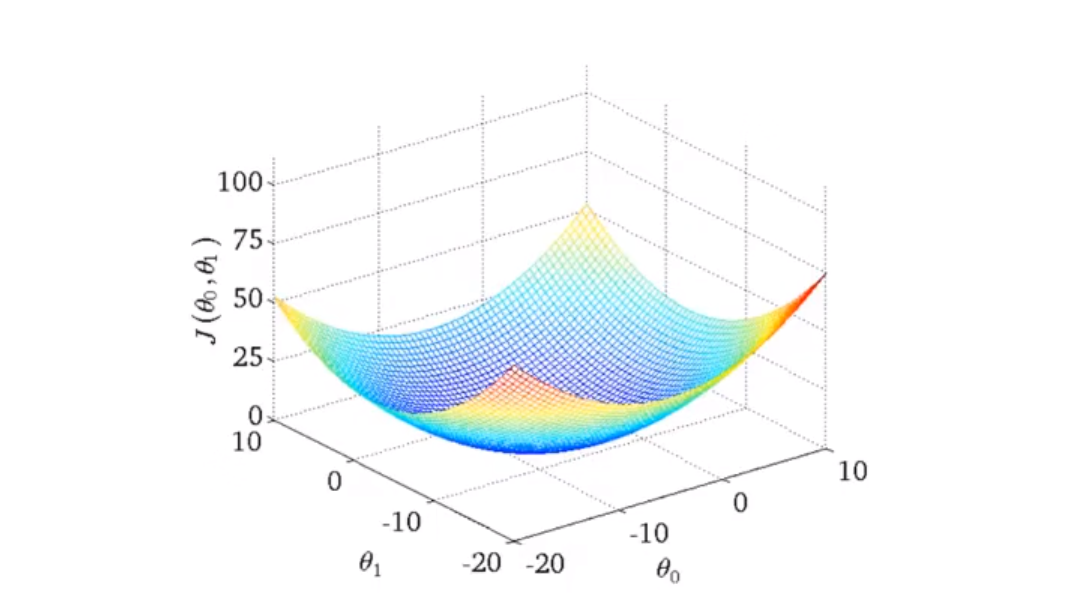
上面这个三维图像就是形成的代价函数 J

然后再是等高线图（等 高图像）

相当于把之前的三维图像进行平面化得到的是上右图，

上面不同的点会对应\theta_1 和\theta_0 从而得到相对应的代价函数，来求解。

因为其具备连续可导性，所以会有一个最优解

梯度下降法

让代价函数 J 最小化（minimizing）

从设置一个初始值开始（\theta_1 = 0(斜率) \theta_0 = 0(截距)）

然后改变这两个值，直到找到最小值，（局部最小值）

梯度是方向导数的最小值，所以如果起始点偏移了一点，得到的结果是完全不同的局部最优解

$$ \theta_j:=\theta_j-\alpha\frac{\sigma}{\sigma\theta_j}J(\theta_0 , \theta_1) $$ 上面这个公式就是优化公式，注意 := 代表的赋值运算。

并且在计算过程中，\theta_1 和 \theta_0 的变化应该是同步进行的，如果不是同步进行就会导致出错

关于上面计算公式中的 alpha 这个称为学习速率，改变这个的数值，会导致进度的加快或者减慢，

这个数能控制我们以多大的幅度来更新这个参数 \theta_ j

simultaneously update （同时更新数据）

之前函数中的偏导项是为了确定下降最快的方向

---

上面就是 \alpha 太大或者太小的情况

如果假设 \theta_1 的初始值已经在最优解（局部最优解）上，那么下一步应该是什么样的

很明显，在局部最优点的导数等于 0 ，

事实上，当在更新\theta_ 1 的时候，由于其发生了变化，再一次变化之后得到的新的 J(\theta_1) 所对应的那一点的斜率（导数）会自动减少， 所以其减小的速率也会随之减小。 正如上图所示：↑

综上，我们可以来尝试最小化任何的代价函数 J

非线性回归的梯度下降

$$\text{原推导公式 ：}{\theta }_j:={\theta }_j-\alpha \frac{\sigma }{\sigma {\theta }_j}J({\theta }_0,{\theta }_1)$$

将之前的代价函数和上面所讲到的梯度下降法结合起来，就能得到下面这个公式推导：

$$\begin{array}{rl}\frac{\sigma }{\sigma {\theta }_j}J({\theta }_0,{\theta }_1)& =\frac{\sigma }{\sigma {\theta }_j}\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)}-y^{(i)}){)}^2\\ & =\frac{\sigma }{\sigma {\theta }_j}\frac{1}{2m}\sum _{i=1}^m({\theta }_0+{\theta }_1{x}^i-y^i{)}^2\end{array}$$

那么对于两个变量来说，算法中会连续对两个变量进行计算：

$$\text{这个是对j=0 }\mathrm{也}\mathrm{就}\mathrm{是}\mathrm{对}{\theta }_0\mathrm{求}\mathrm{偏}\mathrm{导}\mathrm{之}\mathrm{后}:\frac{\sigma }{\sigma {\theta }_0}J({\theta }_0,{\theta }_1)=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})$$$$\text{这个是对j=1 }\mathrm{也}\mathrm{就}\mathrm{是}\mathrm{对}{\theta }_1\mathrm{求}\mathrm{偏}\mathrm{导}\mathrm{之}\mathrm{后}:\frac{\sigma }{\sigma {\theta }_1}J({\theta }_0,{\theta }_1)=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x^{(i)}$$

注意平方，平方是个很神奇的东西：

$$\begin{array}{c}\mathrm{举}\mathrm{个}\mathrm{例}\mathrm{子}：\\ \mathrm{针}\mathrm{对}(x+2y{)}^2\mathrm{对}x\mathrm{求}\mathrm{偏}\mathrm{导}：\\ \mathrm{结}\mathrm{果}\mathrm{是}：2(x+2y)\\ \mathrm{也}\mathrm{就}\mathrm{是}\mathrm{说}\mathrm{因}\mathrm{为}\mathrm{平}\mathrm{方}\mathrm{的}\mathrm{存}\mathrm{在}，\mathrm{在}\mathrm{上}\mathrm{面}\mathrm{的}\mathrm{对}{\theta }_0\mathrm{求}\mathrm{偏}\mathrm{导}\mathrm{的}\mathrm{时}\mathrm{候}\\ \mathrm{因}\mathrm{为}\mathrm{其}\mathrm{系}\mathrm{数}\mathrm{为}1，\mathrm{也}\mathrm{就}\mathrm{导}\mathrm{致}\mathrm{了}\mathrm{结}\mathrm{果}\mathrm{为}1\mathrm{乘}\mathrm{以}\mathrm{他}\mathrm{本}\mathrm{身}(\mathrm{平}\mathrm{方}\mathrm{里}\mathrm{面})\end{array}$$

需要注意的是对\theta_1 进行求偏导之后，因为h(x)是一个关于x的函数，相当于复合函数求偏导，结果是要乘以x^(i)的

重复上面的步骤，一直收敛，直到找到最优解

---

对于上面的这个图像(bow-shaped function) 又叫做弓状图，是关于(\theta_1,\theta_0)的凸函数

不同于之前的函数，这个会找到全局最优解，因为没有其他的局部最优解

---

对于上面提到的函数，我们有时候也会称其为Batch梯度下降

这个算法会全览整个训练集

有关于Batch ：这个代表着遍历一遍整个数据集，当然也有其他的形式的方式

有些其他的算法不会遍历整个训练集。

关于矩阵和向量（matrix）

Matrix : Rectangular array of numbers 指的是矩形数组

接下来是表达矩阵中特定元素的方法：

The standard notation is ：

需要注意的是，矩阵的开始是从 1 开始的，而不是0

关于向量，向量是一个只有一列的矩阵

注意是一列 上面这个例子代表的就是一个四维的向量，the one ,two ,three and so on .

此外

我们通常用大写的A、B、C、.....来表示矩阵，而小写的字母a、b、c、.....来表示其中的数字

矩阵的加法和乘法以及数和矩阵的乘法

关于加法：

矩阵的加法只能是具有相同性质的矩阵（相同的shaped）才可以相加

并且相加的规则是每个位置上的元素对应相加，比如说第一列第一行的元素要和第一列第一行的对应的元素进行相加

矩阵和标量的乘法运算

这个地方的标量可能是代表的一个复杂的结构或者一个数字或说是一个实数(real number)

上面这是一个简单的混合运算。会得到一个三维向量

矩阵向量相乘

从特例开始：（矩阵向量相乘）

一个三行二列的矩阵和一个二行一列的矩阵(二维向量)继续相乘，得到的是一个三行一列的矩阵(三维向量)

更详细的解释：

计算方法就是将矩阵中的每一行中的每一个元素与向量的每一个元素进行相乘然后再全部相加起来，就是得到向量的那一行的结果。以此类推，最终得到一个与之前矩阵行数相同维度的向量。

另外一个例子：

结果是显而易见的

A neat trick(小技巧)

简单的来讲，就是将多个数字进行矩阵化

$$\text{例如上面的：}\left[\begin{array}{c}2104\\ 1416\\ 1534\\ 852\end{array}\right]\text{就可以换成}\left[\begin{array}{cc}1& 2104\\ 1& 1416\\ 1& 1534\\ 1& 852\end{array}\right]$$

然后再进行计算：

$$\left[\begin{array}{cc}1& 2104\\ 1& 1416\\ 1& 1534\\ 1& 852\end{array}\right]\times \left[\begin{array}{c}-40\\ 0.25\end{array}\right]=\left[\begin{array}{c}-40\times 1+0.25\times 2104\\ -40\times 1+0.25\times 1416\\ ...\\ ...\end{array}\right]$$

就这样得到了最终的结果。

如果我们需要计算很多次，那么就可以利用这样的一个方程来进行简单化处理，这样比手动的加起来会方便很多。

矩阵乘法

两个矩阵相乘的原理：

实际上一个 N times M 乘以 X times y is N times Y

注意计算过程中是，对应位置上的数进行相乘

$$\mathrm{比}\mathrm{如}：\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]\times \left[\begin{array}{cc}A& B\\ C& D\end{array}\right]=\left[\begin{array}{cc}a\times A+b\times C& a\times B+b\times D\\ c\times A+d\times C& c\times B+d\times D\end{array}\right]$$

上面这个就是其计算根本

把矩阵相乘拆成两个矩阵乘以向量，然后再合起来。

需要注意的是，**矩阵相乘需要维度匹配，简单来说就是$m\times n\ast n\times a=m\times a$

再来一个例子：

再结合之前的分析：

通过这样的一个矩阵相乘运算就可以得到不同的计算方式而来的结果。

在不同的语言中会有很多很好的线性代数库 （神奇的算法）

关于矩阵乘法的特性

在实数的乘法运算中，乘法具有可颠倒性。

但是在矩阵乘法中，乘法的顺序是不能随便颠倒的

数乘的结合律

在矩阵乘法中同样适用

在实数运算中，会有一个实数单位：1

也就是 1 × z = z

那么在矩阵运算中，同样的有一个单位矩阵

其特征就是沿对角线上都是 1 ， 其他位置上都是 0

同样的 单位矩阵乘以任意的矩阵，结果都是其本身

一定要注意的是，关于 单位矩阵 I 他需要满足 A矩阵的形式

正如上面截图中的所演示的那样。要灵活改变单位矩阵 I 的shaped

逆 和 转制(特殊矩阵运算)

逆矩阵

$$\begin{gathered} A\times B=E=>B\mathrm{是}A\mathrm{的}\mathrm{逆} \\ \text{E 就是单位矩阵} \end{gathered}$$

上面这个就是计算逆矩阵的方法,借用的是单位矩阵

在实数中的逆运算,方法是通过利用单位 1 来进行计算 :但是不是所有的实数都有,就像 0

注意只有方阵才会有逆矩阵,方阵也就是row == col

一个简单的例子：

在很多的计算软件中都会有 计算这样的算法

但这些算法受限于计算精度,可能不会生成 0 但是会接近于 0 进行(圆整)

同样的,也有一些矩阵是没有逆矩阵的，被称为“奇异矩阵”（singular）或者“退化矩阵”（degenerate）

转置运算

上面这个是转置运算的结果 ↑

简单来说就是将一个矩阵的行和列倒换位置

由原来的 n × m 转变为 m × n

多功能（多元）

一种新的线性回归

这部分需要注意的地方是，这是在告诉我们当使用一个新的机器学习算法的时候，需要注意数据输入的格式，这非常重要。这直接决定了我们后续应该怎么处理这些数据

适用于多个变量或者多特征量的情况

一些简单的表示方法👆

$$x_3^{(2)}\mathrm{就}\mathrm{代}\mathrm{表}\mathrm{第}\mathrm{二}\mathrm{组}\mathrm{特}\mathrm{征}\mathrm{的}\mathrm{第}\mathrm{三}\mathrm{个}\mathrm{特}\mathrm{征}\mathrm{值}$$

接下来是对多特征值表示的简答方法：

其精髓在于设置 x_0 = 1 ,这样就形成了两个一般大小的矩阵。

然后再对 \theta 矩阵进行转置运算，（将行和列倒换）

梯度下降处理多元线性回归

这里有的参数是\theta_0 到 \theta_n 但是我们不把它看作是n个独立的参数（尽管这是可以的）

我们把这些参数看作是一个 n+ 1 维的 \theta 向量

我们把此模型的参数看作是一个向量

下面就是多元线性回归的方程

上面的都是已经求完导之后的结果，可以看出来尽管是多元线性回归方程，结果也和一元函数差不多

我们可以认为**“一元可以看作是多元的特殊情况，多元看作是一元的推广”**

事实上，我们可以看到这个在推广的过程中差不多都是类似的

在\theta_0的哪里，我们规定了 x_0^(i) = 1

特征缩放（实用技巧）

主要目的是为了让多个特征值都处在一个相近的范围内。

这样梯度下降法就能更快的收敛

就像在上面这个的例子里面，我们通过利用归一化处理，将这两个特征值进行放置到-1 ~ 1之间来进行处理，这样的话，可以让\theta_0 和 \theta_1 的取值更加贴合，从而能更快的收敛、更好的进行计算。

关于是否要进行归一化处理，可以根据经验来进行判断，只要不是差距特别大， 一般都是没有什么问题的。

有关于 Mean normalization（均值归一化）

正态分布标准化

至于为什么会将归一化放到 0 附近，其原因是让坐标原点放到一堆数据的中间。

如何选择学习率

学习率就是之前所说的 梯度下降法 中前面的那个系数 \alpha

---

代价函数随着迭代步数增加的变化曲线

通过这个曲线来判断梯度下降算法是否已经收敛

同样的，可以设置一个最小值来自动判断是否已经实现了收敛 ， 但是这个最小值并不好判断

上面这个函数的横坐标是迭代次数，纵坐标是代价函数的值

而学习率过大会导致代价函数发散

无论是出现了那种情况，只要是代价函数没有成功的下降，那么一定是 \alpha 太大，这个时候就需要减小 \alpha 的值

但是\alpha 的值如果太小的话，就会导致梯度下降算法的收敛变的很缓慢

所以我们一般都会绘制 代价函数随迭代步数变化的曲线

这里会有一些关于如何选择 \alpha 的方法，可以按照吴恩达给出的方法来进行测试。

至于为什么会是 3

将0.01开根号之后接近 3

特征和多项式回归

就是关于特征的选择

上面就是一个example，我们可以设置一个房子的长度和宽度是两个特征，同样的道理我们也可以用一个面积来当作特征值

这取决于我们自己的选择，选择哪种特征更合适。

选择面积，尽管面积相同，但是房子的形状不会一样，所以是否要选择，需要根据实际情况

---

关于多项式回归，针对一个特征值上的点，并不是线性的，我们可以用多项式展开来进行拟合

这个地方的多项式，有一点 泰勒 的味道，泰勒是在某一点上的拟合。

---

在上面图片中的预测中，如果选择使用 二次函数来进行拟合，可能会出现随着面积增大，房价下降的情况。

所以会选择三次函数来进行拟合

同样的，关于上面的这个特征值，三个的范围差距就很大，所以特征放缩就很重要。

这样才能将值的范围变得具有可比性

对于上面的拟合，同样的，也可以选择不使用三元函数来进行拟合：

当然也可以选择 对数形式的函数来进行拟合，

这完全取决于对函数图像的了解程度和对数据的形状的了解

根据实际情况来选择函数模型

现在我们可以自由选择使用什么样的特征并且通过设计不同的特征，能够使用更复杂的函数来拟合数据

正规方程

是一种对于某些线性回归问题，会给我们一种更好的方法来求得最优解

这是一种解析算法

只需要 one step？

事实上上面图中的这个算法就是逐个对 \theta 进行求偏导数，将**偏导数 等于 0 ** 从而求出最优解，但是这样会很复杂

$$\mathrm{关}\mathrm{于}：\theta =(X^{T}X{)}^{-1}{X}^{T}y$$

这个方程的解是如何推导出来的，之后的视频中会讲到。

上面图片中转置后的结果应该是（应当特别注意转置和求倒数是不一样的）

$$X=\left[\begin{array}{cc}1& x_1^1\\ 1& x_1^2\\ 1& x_1^3\\ ...& ...\\ 1& x_1^m\end{array}\right]$$

这里的$\theta$ 指的是 目前的最小特征，也就是最优解$\theta$。

（最小二乘法）？

$$\begin{array}{c}\mathrm{关}\mathrm{于}\theta =(X^{T}X{)}^{-1}{X}^{T}y\\ \mathrm{这}\mathrm{个}\mathrm{公}\mathrm{式}\mathrm{里}\mathrm{面}\mathrm{的}(X^{T}X{)}^{-1}\mathrm{是}{X}^{T}X\mathrm{的}\mathrm{逆}\mathrm{矩}\mathrm{阵}\\ X^{T}X\mathrm{一}\mathrm{定}\mathrm{要}\mathrm{是}\mathrm{方}\mathrm{阵}\mathrm{才}\mathrm{能}\mathrm{有}\mathrm{逆}\mathrm{矩}\mathrm{阵}，\mathrm{这}\mathrm{就}\mathrm{要}\mathrm{求}X\mathrm{的}\mathrm{行}\mathrm{向}\mathrm{量}\mathrm{不}\mathrm{能}\mathrm{大}\mathrm{于}\mathrm{列}\mathrm{向}\mathrm{量}\\ \mathrm{另}\mathrm{外}{X}^{T}X\mathrm{不}\mathrm{能}\mathrm{为}0，\mathrm{这}\mathrm{就}\mathrm{是}\mathrm{最}\mathrm{小}\mathrm{二}\mathrm{乘}\mathrm{法}\mathrm{的}\mathrm{局}\mathrm{限}\mathrm{性}\end{array}$$

假如要使用正规方程来进行求解\theta，那么就不需要进行特征放缩

关于梯度下降和正规方程的优缺点

梯度下降需要这是$\alpha$,同时还需要很多次的迭代，

而正规方程不需要以上，但是事实上，当n（特征数量）非常大的时候，依然需要使用梯度下降，而不是正规方程。

非常大的时候，梯度下降会比正规方程的计算速度快，同样的，当n没有很大的时候，使用正则方程会很方便的解出\theta值

所以在特征值数量比较少的情况，选择正规方程法算是一个比较好的方法，但是如果特征值的数量特别大，选择梯度下降法或者其他的一些别的算法可能会更好

并且，正规方程法其实也不适用于其他的一些更复杂的算法，所以梯度下降法真的是一个比较好的方法

当在矩阵不可逆的情况下

第一种情况就是存在冗余的特征

比如说 x_1 是平方米、x_2 是平方英米，

这两个特征之间存在一个绝对的关系方程

线性相关之后在进行初等变化的时候，就会发生秩小于n，导致其矩阵不可逆

不是满秩，不可逆

这样会满足线性相关，从而导致矩阵不可逆

第二种情况

有太多的特征

简单来说就是存在 M ≤ N （PS:M是训练样本，N是特征数量）

针对这种情况，我们会考虑使用删除一部分特征，或者使用后面会学到的 正则化

MatLab使用(octave)

基本操作

加减乘除就不用说了，就是简答的操作。

随机数

rand()

下面这个是randn()

w = randn(1,6)
生成的数是一个1 times 6 的一个矩阵
这个满足高斯分布，其标准差或者方差为1

w = -6 + sqrt(10)*(randn(1,10000))
hist(w)
这样会绘制一个针对随机变量W的直方图
其均值为 -6  因为是从  -6  开始加的.
且因为是 sqrt(10) ，所以高斯随机变量的方差为 10  标准差为 sqrt(10)

可以看出来其是符合高斯分布的。（正态分布）

我们也可以给与其参数

比如：
hist(w,50)
上面这个就是绘制了一个有50个竖条的直方图

生成单位矩阵

所用的函数为
eye(4)
结果为
ans =

     1     0     0     0
     0     1     0     0
     0     0     1     0
     0     0     0     1

移动数据（操作数据）

关于矩阵的一个小操作：

大小（长度）

>> A =

     1     2
     3     4
     5     6

>> size(A)

ans =

     3     2

>> SZ = size(A);
>> SZ

SZ =

     3     2

>> size(SZ)

ans =

     1     2

>> size(A,1)
//这个是代表输出A矩阵的第一维度的大小

ans =

     3

最大长度

>> V = [1 2 3 4];
>> length(V)

ans =

     4
//输出的是最长维度的大小

文件路径

>> pwd

ans =

    'E:\MATLAB学习文件\Machine Leaning'
//pwd函数返回的是当前所在的文件路径

加载文件

使用的是
load 函数
load 文件名字包括扩展名
还可以
load('文件名字包括扩展名')
这样是以字符串的形式来加载文件，最终会以文件名（不包含扩展名）为变量保存在内存中。

变量信息

使用 whos 函数来展示当前内存中所存在的所有变量以及其详细信息
>> whos
  Name      Size               Bytes  Class     Attributes

  A         3x2                   48  double              
  SZ        1x2                   16  double              
  V         1x4                   32  double              
  a         1x1                    8  double              
  ans       1x29                  58  char                
  b         1x2                    4  char                
  w         1x10000            80000  double              

同样的
使用  who  函数就是仅仅展示其所存在有哪些变量。

删除变量

使用的函数为 
clear 变量名称

保存变量

可以直接用赋值的方式来存储
比如
v = V(1:10)
上面这个的含义就是将 V 变量中的前 10 个元素赋值给了 v

如果说我想要保存到硬盘中

可以使用下面的语句
save 文件名.mat 变量名称
//这个文件会保存在当前的文件路径 也就是之前 pwd 函数所展示的路径下面。

删除所有变量

clear
这个方法就会删除现在内存中所有的变量

索引

>> A

A =

     1     2
     3     4
     5     6

>> A(3,2)

ans =

     6

>> A(:,2)

ans =

     2
     4
     6

上面函数中的 : 代表的是在这一行或者一列中的所有元素(means every element along that row/column)

>> A([1,3],:)

ans =

     1     2
     5     6

上面的这个操作就是生成索引为 1 和 3 的那一行中的所有的 列 元素

上面这种复杂的矩阵索引操作并不会很常用

进行赋值操作与扩展

>> A(:,2) = [10,12,11]

A =

     1    10
     3    12
     5    11

这个就是将第二列中的所有行元素进行赋值转换成其他

---

>> A = [A , [100;101;102]];
>> A

A =

     1    10   100
     3    12   101
     5    11   102

将A矩阵向右添加一列，（注意其大小应该与原矩阵相符）

---

>> A = [A ; [100 101 102]];
>> A

A =

     1    10   100
     3    12   101
     5    11   102
   100   101   102

上面这个语法就是向下扩展一行（向上同理）

转换为一列

>> A(:)

ans =

     1
     3
     5
    10
    12
    11
   100
   101
   102

合并矩阵

>> C =[A B]

C =

     1     2    11    12
     3     4    13    14
     5     6    15    16

>> C = [A ; B]

C =

     1     2
     3     4
     5     6
    11    12
    13    14
    15    16

分别是左右合并，上下合并，是由顺序的，按照前后顺序来排列

计算数据

矩阵相乘

注意相乘是要求n by m times a by b （m == a)

计算方法是 A * B

>> A = [1 2; 3 4 ; 5 6]

A =

     1     2
     3     4
     5     6

>> B = [3 2;6 7]

B =

     3     2
     6     7
     
>> A * B

ans =

    15    16
    33    34
    51    52

上面这个是矩阵的乘法

下面这个是矩阵点乘，也就是对应矩阵位置上的元素进行相乘，也就是说需要 两个矩阵的大小一样维度一样。

计算方法是 
A .* B

同样的还有很多类似的运算，比如说

./ 每个元素进行除法运算，（比如取倒数，1 ./ V）

.^ 每个元素进行幂运算

对数与指数

log(10)
这个默认代表的是以e为底的10的对数
>> log(10)

ans =

    2.3026

如果换成  log2（10）
这个代表以2为底的10的对数
>> log2(10)

ans =

    3.3219

而关于指数运算

用到的函数是  exp(x)
这个代表的是
e^x
>> exp(1)

ans =

    2.7183

绝对值

abs()
无论是什么对象，返回的就是其绝对值
包括矩阵、向量等等

矩阵的转置运算

>> A

A =

     1     2
     3     4
     5    10

>> A'

ans =

     1     3     5
     2     4    10

用到的就是 单引号 '

max和返回index

>> a = [1 15 2.9 3]

a =

    1.0000   15.0000    2.9000    3.0000

>> max(a)

ans =

    15

>> [val ,ind] = max(a)

val =

    15


ind =

     2

需要注意的是这个索引是从 1 开始计算的

---

如果是针对矩阵使用max()函数，返回的会是每一列中的最大数值
例如：
>> A

A =

     1     2
     3    19
     5    10

>> max(A)

ans =

     5    19

同样的

max(A,[],2)
返回的是在第2维度，也就是  行  
中取出所有的最大值。
1  是代表第一维度，也就是  列
所以返回的是  行  ，将所有的列中的最大元素取出组成一行
>> A

A =

     1     2
     3    19
     5    10

>> max(A,[],1)

ans =

     5    19

比较 (逻辑运算)

>> a

a =

    1.0000   15.0000    2.9000    3.0000

>> a < 3

ans =

  1×4 logical 数组

   1   0   1   0

找索引

使用的函数是
find()
比如说
>> find(a<3)

ans =

     1     3

返回的是那个元素所在的索引

幻方矩阵

magic()
>> c = magic(4)

c =

    16     2     3    13
     5    11    10     8
     9     7     6    12
     4    14    15     1

幻方矩阵有一个特殊的特点，

也就是每一行每一列每一条对角线上的元素相加都是相同的数

我们可以利用sum函数是求和来计算一下

>> F = magic(9)

F =

    47    58    69    80     1    12    23    34    45
    57    68    79     9    11    22    33    44    46
    67    78     8    10    21    32    43    54    56
    77     7    18    20    31    42    53    55    66
     6    17    19    30    41    52    63    65    76
    16    27    29    40    51    62    64    75     5
    26    28    39    50    61    72    74     4    15
    36    38    49    60    71    73     3    14    25
    37    48    59    70    81     2    13    24    35
    
>> sum(F，1)

ans =

   369   369   369   369   369   369   369   369   369

>> sum(F,2)

ans =

   369
   369
   369
   369
   369
   369
   369
   369
   369
   
那么怎么计算对角线上的元素相加呢
利用eye()函数来计算。


>> eye(9)

ans =

     1     0     0     0     0     0     0     0     0
     0     1     0     0     0     0     0     0     0
     0     0     1     0     0     0     0     0     0
     0     0     0     1     0     0     0     0     0
     0     0     0     0     1     0     0     0     0
     0     0     0     0     0     1     0     0     0
     0     0     0     0     0     0     1     0     0
     0     0     0     0     0     0     0     1     0
     0     0     0     0     0     0     0     0     1

>> sum(F .* eye(9))

ans =

    47    68     8    20    41    62    74    14    35

>> sum(sum(F.*eye(9)))

ans =

   369
   
   
那么另外一个对角线呢
利用的函数是flipud()
这个函数会将矩阵倒置
>> flipud(eye(9))

ans =

     0     0     0     0     0     0     0     0     1
     0     0     0     0     0     0     0     1     0
     0     0     0     0     0     0     1     0     0
     0     0     0     0     0     1     0     0     0
     0     0     0     0     1     0     0     0     0
     0     0     0     1     0     0     0     0     0
     0     0     1     0     0     0     0     0     0
     0     1     0     0     0     0     0     0     0
     1     0     0     0     0     0     0     0     0
     
>> flipud(A)

ans =

     5    10
     3    19
     1     2

>> A

A =

     1     2
     3    19
     5    10
注意并不是对角线倒置，而是上下倒换
所以我们利用这个特性来计算另外一条对角线
>> sum(sum(F.*flipud(eye(9))))

ans =

   369

求和以及求积

sum()求和
会将里面所有的元素进行相加
prod()求积
同样的也是会将所有的元素进行相乘

如果是对矩阵进行计算，是会将里面的每一列的元素相加或者相乘。

>> A

A =

     1     2
     3    19
     5    10

>> sum(A)

ans =

     9    31

取整

floor()
是向下取整
ceil()
是向上取整

矩阵求逆

用到的函数是pinv()
比如说A * pinv(A)
这样得到的就是单位矩阵
虽然有可能需要将元素进行近似

>> D = magic(3)

D =

     8     1     6
     3     5     7
     4     9     2

>> D * pinv(D)

ans =

    1.0000   -0.0000    0.0000
    0.0000    1.0000         0
   -0.0000    0.0000    1.0000

关于画图

以magic函数为基础的绘制一个灰度图

>> A = magic(5)

A =

    17    24     1     8    15
    23     5     7    14    16
     4     6    13    20    22
    10    12    19    21     3
    11    18    25     2     9
    
imagesc(A),colorbar,colormap gray;

矢量转化

通过进行 向量化 会让计算变得更加简单

下面是一些例子

$$\text{如果要计算这个程序 }{h}_{\theta }(x)=\sum _{j=0}^n{\theta }_j{x}_j$$

我们可以把这个求和转化为两个向量的内积

$$=={\theta }^{T}x$$

上面这两个都是向量。

$$\text{展开来说： }\theta =\left[\begin{array}{c}{\theta }_0\\ {\theta }_1\\ {\theta }_2\end{array}\right]$$

现在的\theta是一个 3 × 1 的矩阵，而x也是一个 3 × 1 的矩阵，这样是不能进行运算的

而我们将 \theta 转置之后就可以了

$${\theta }^T=\left[\begin{array}{ccc}{\theta }_0& {\theta }_1& {\theta }_2\end{array}\right]$$

转置之后就成了一个 1 × 3 的矩阵，就满足了矩阵的乘法。

这样会很方便

---

那关于我们的梯度下降法来说，利用向量化同样的会让我们的程序变得更简洁和更快。

注意，下面的这些方程都是在求完偏导数之后的

思路是

$$\theta :=\theta -\alpha \delta$$

需要注意的是这里面的$\theta$和$\delta$都是向量\alpha 则是一个常数 R

同时

$$\delta =\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x^{(i)}$$

这里面的

$$(h_{\theta }(x^{(i)})-y^{(i)})\text{ 是一个常数}$$$$x^{(i)}=\left[\begin{array}{c}{x}_0^{(i)}\\ x_1^{(i)}\\ x_2^{(i)}\end{array}\right]$$$$\text{对于不同的i来说}(h_{\theta }(x^{(i)})-y^{(i)})\mathrm{确}\mathrm{实}\mathrm{不}\mathrm{是}\mathrm{同}\mathrm{一}\mathrm{个}\mathrm{值}，\mathrm{但}\mathrm{是}\mathrm{确}\mathrm{实}\mathrm{是}\mathrm{一}\mathrm{个}\mathrm{实}\mathrm{数}，$$$$\begin{array}{c}\text{但是对于后面的}{x}^{(i)}=\left[\begin{array}{c}{x}_0^{(i)}\\ x_1^{(i)}\\ x_2^{(i)}\end{array}\right]\\ \text{其表示的是第i组样本中的所有特征值，所以其维度和}\theta \mathrm{一}\mathrm{样}\mathrm{都}\mathrm{是}n+1\end{array}$$

---

$$\mathrm{推}\mathrm{导}\mathrm{了}\mathrm{好}\mathrm{久}，\mathrm{先}\mathrm{说}\mathrm{结}\mathrm{果}：\delta =\frac{(X^T((X\theta {)}^{(n)}-y^{(n)}))}{m}$$

上面的这个结果其实就是根据之前的那个例子来推导出来的

求和转化为两个向量相乘。

合并一下：

$$\theta :=\theta -\alpha \frac{(X^T((X\theta {)}^{(n)}-y^{(n)}))}{m}$$

分类

好与坏、以及各种分类问题

目前我们先考虑二元分类的问题。

如果是用线性回归的方法来进行预测

通过现有的数据集来训练出来的拟合直线会受到偏差值的影响，从而导致拟合出来的直线是不准确的

所以一般不用线性回归来进行分类问题

接下来的视频中，会使用 logistic回归来进行拟合，虽然叫做拟合，但是实际上是分类问题。

这个回归算法会让结果的值保证在 0 到 1 中

Logistic Regression（对数回归）

在分类问题中，如何选择合适的方程来展示

我们希望输出值在 0 到 1 之间。

利用的就是g()方程

这个方程叫做sigmoid函数，同时也叫做logistic函数。

这个是函数图像

$$\text{函数方程为：}g(Z)=\frac{1}{1+e^{-Z}}$$

中间的变化大，两端的变化小，同时这个函数的值必定在 0 到 1 之间。

最终得到的结果是：

$$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$$

---

上面的方程中，假设输入的是一个x_1(tumor size)，通过函数的转变之后，能得到结果为0.7，是恶性肿瘤的概率为0.7

决策边界(decision boundary)

这个能更好的帮助我们理解假设函数h(x)在计算什么

在上面的计算中，如果我们需要让y = 1 或者y = 0 ，其就是要Z>=0.5或者Z<0.5

假设我们已经知道\theta的取值了，那么我们利用之前的方法，如果想要y = 1那么其结果就是

-3x_0+x_1+x_2，这里面x_0取值为1（这是规定）

那么通过这样的计算，我们就可以得到一条直线：

$$x_1+x_2=3$$

这条直线就能比较好的将两个区域进行区分

至于其\theta值是如何取到的，未来会讲到

针对于上面这种的形状，我们可以像之前那样利用多项式回归来进行回归(加上一些更高次的变量)

比如先这样：

$$h_{\theta }(x)=g({\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_1^2+{\theta }_4{x}_2^2)$$

这样一来，我们就有四个\theta需要设置

我们在这里先设置

$$\begin{gathered} {\theta }_0=-1 \\ {\theta }_1=0 \\ {\theta }_2=1 \\ {\theta }_3=1 \end{gathered}$$

那这样一来，想要“y = 1”得到的结果就是

$$-1+x_1^2+x_2^2>=0$$

转化一下就是一个标准圆

决策变量不是训练集的属性，而是假设本身及其参数的属性

准确的说，我们是用训练集来拟合参数\theta

同样的，我们可以使用具有更多特征的高阶多项式来进行拟合，这样就可以得到一个更加复杂的决策边界

需要注意的是

$$\begin{array}{c}{h}_{\theta }(x)=g({\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_1^2+{\theta }_4{x}_2^2)\text{这个里面的}g(x)\\ \mathrm{其}\mathrm{实}\mathrm{就}\mathrm{是}{\theta }^{T}x\mathrm{的}\mathrm{展}\mathrm{开}\mathrm{式}\\ \mathrm{而}{h}_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}\mathrm{是}\mathrm{不}\mathrm{需}\mathrm{要}\mathrm{求}\mathrm{解}\mathrm{出}\mathrm{来}\mathrm{的}\mathrm{我}\mathrm{们}\mathrm{根}\mathrm{据}\mathrm{的}\mathrm{是}\mathrm{这}\mathrm{个}\mathrm{函}\mathrm{数}\mathrm{的}\mathrm{图}\mathrm{像}\mathrm{性}\mathrm{质}\\ \mathrm{根}\mathrm{据}\mathrm{的}\mathrm{就}\mathrm{是}\mathrm{当}({\theta }^{T}x)>0\mathrm{的}\mathrm{时}\mathrm{候}，y\mathrm{是}\mathrm{大}\mathrm{于}0.5\mathrm{的}，\mathrm{甚}\mathrm{至}\mathrm{趋}\mathrm{近}\mathrm{于}1\mathrm{的}\\ \mathrm{而}\mathrm{当}({\theta }^{T}x)<0\mathrm{的}\mathrm{时}\mathrm{候}，y\mathrm{是}\mathrm{小}\mathrm{于}0.5\mathrm{的}，\mathrm{甚}\mathrm{至}\mathrm{是}\mathrm{趋}\mathrm{近}\mathrm{于}0\mathrm{的}\end{array}$$

代价函数(cost function)

将代价函数抽象出来成为一个单独的函数

如果我们按照之前的方法(线性回归)来求解全局最优解，那么得到的会是凸函数，也就是会有很多的局部最优解，很难找到那个全局最优解。

其原因在于h(x)是一个非线性的函数

$$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$$

---

上面这个方程就是我们要用到logistic回归上面的代价函数

下面解释为什么

太巧妙啦！

整个图像其实就是代价函数，利用这个函数的特点，产生相应的代价，从而使其能够更好的训练

如果我们的h(x) = 1 那么代表着我们的代价为0，这说明我们的预测是完全正确的，因为已经知道前提是y=1了

那反过来，如果h(x) = 0 那么代表着我们的代价将会是 无穷大，这样的话，可以说明我们这个预测就是非常失败的，所以其代价函数的值会非常大。

h(x)其实就是代表着预测的结果，而在这里的 y 代表的其实是实际上的结果（已知的）

当 y =0 的时候，那么其实形式是一样的，也能得到与 y = 1 的时候相类似的结果。

基于以上的思想，再利用梯度下降方法，从而得到logistic回归算法

用一种更简单的方法来表示代价函数

以及如何运用梯度下降方法来拟合出logistic回归的参数

这里的 J(\theta) 其实代表代表的是：每一个参数在通过代价函数之后产生的代价的总和

但是上面的公式中，其实会发现是把方程根据y的取值分成了两部分

这样其实是不方便的

接下来将其合并到一起

$$Cost(h_{\theta }(x),y)=-y\times log[h_{\theta }(x)]-(1-y)\times log[1-h_{\theta }(x)]$$

其实可以发现就是利用的 y 不是 1 就是 0 的特点，将两个公式进行了合并

$$\begin{array}{}\text{(1)}& \mathrm{当}y=1\mathrm{的}\mathrm{时}\mathrm{候}：Cost(h_{\theta }(x))=-log[h_{\theta }(x)]\end{array}$$$$\begin{array}{}\text{(2)}& \mathrm{当}y=0\mathrm{的}\mathrm{时}\mathrm{候}：Cost(h_{\theta }(x))=-log[1-h_{\theta }(X)]\end{array}$$

下面就是将其合并到J(\theta)中之后：

上面这个方程是通过统计学中的最大似然估计得出的

需要注意的是在上面的公式中提出来了一个负号，前面的系数从 1/m 变成了 -1/m

为了拟合出合适的参数，找到让 J(\theta) 取得最小值的参数 \theta

然后再利用这个 \theta 值来预测出新的一组 x 值，

这个值认为是 当 x = 0 的时候，y = 1 的概率大小

下面是使用梯度下降法

这个求导还是比较复杂的：

这个方程可以进行展开：（将 h(x) 带入方程中）

$$\begin{array}{rl}J(\theta )& =-\frac{1}{m}[\sum _{i=1}^m{y}^{(i)}log{h}_{\theta }(x^{(i)})+(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]\\ & =-\frac{1}{m}[\sum _{i=1}^m{y}^{(i)}log[\frac{1}{1+e^{-{\theta }^{T}x}}]+(1-y^{(i)})log(1-\frac{1}{1+e^{-{\theta }^{T}x}})]\end{array}$$

那么其实说白了就是对上面这个方程进行求导运算，具体过程在这里就不在进行展示，因为用公式敲上是非常耗费时间的

下面就是对其进行求偏导数的结果

$$\frac{\delta }{\delta {\theta }_j}J(\theta )=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\times x_j^{(i)}$$

将其放到repeat里面去：

这样就可以针对不同的 \theta值求出其最优解

并且！我们可以注意到这个结果和之前线性回归求得的结果神奇的一样，都是这个公式

其实上我们可以进行推广，比如说我们还有另外的一个公式也是来求极小值的

那么我们就必须要保证假设函数在代价函数处理之后是线性的，否则就不能保证唯一极小性

那既然都是线性的，自然代价函数相近

但其实上，上面公式中的h(x)是发生了变化的，之前线性回归的函数和现在的h(x)是不一样的

所以尽管代价函数在形式上是差不多的，但是实际上假设函数的定义是发生了变化的

在循环变化 \theta 值的过程中，我们也可以使用向量化的方法来实现同时变化，提高效率

高级优化

一般这是用在特征量非常大的情况下。

你像上面提到的这几个算法，优点很明显，甚至不需要设置学习率，也比之前的算法速度更快。

但是同样的，这会更复杂

下面是一个非常简单的例子：

两个特征值，分别对其进行求偏导数，然后再分别等于0，最后

上面这叫做 无约束最小化函数

zeros（2，1）代表的是生成一个初始化的空向量，再往里面填充数

利用的就是上面的这两段指令，进行运行，会得到最优化的结果

需要注意的是，在matlab中，100要以整型的方式输入，而不是字符串型

options = optimset('GradObj','on','MaxIter',100);

多类别分类（逻辑回归）

一个分类方法叫做：“一对多”分类

比如说多种类别的邮件进行分类。

运用的原理如下：

就是依旧是两两分类。

拟合出三个分类器

每个分类器都针对其中一种情况进行训练

当我们需要对x值进行预测的时候，只需要把x值输入到这三个分类器当中，比较这三个分类器给的结果可信度最高、效果最好的一个即可

总结一下，对于预测未知的x代表的值，我们分别进行不同的分类器计算，比较不同的分类概率是多少，取最大值即可。

过拟合问题

过拟合会导致最终的结果欠佳。

下面展示什么是过拟合

以及什么是欠拟合，偏差（bias）

对于欠拟合来说，存在高的偏差

对于过拟合来说，存在着“高的方差”（是可以计算出来的)，也就是虽然每个样本都能很好的描绘出来，但是在整个范围内的曲线是不太好的，甚至可以说是非常曲折的

简单来说过拟合就是没有足够的数据来约束整个的发展。

在公式上展示就是cost function（代价函数）训练到最后得到的结果就是接近于0，甚至是等于0

过拟合运用的变量太多，千方百计地区拟合训练集，导致最后的泛化性（对待新数据）非常差

对于逻辑回归也是同样的道理：

可以使用专门的工具来实现识别过拟合和欠拟合的问题

有一种方式是绘制出最终的预测曲线，但实际上这个方法并不适用。因为在一个训练的过程中，很有可能会有很多的特征变量，这会导致绘图变得非常困难。

这里有两个方法来减少过拟合的情况

一种方法是尽量减少选取变量的数量

具体而言 ， 可以人工检查变量清单 ，人工选择哪一个变量更重要 ，选择一些有影响力更大的变量，删掉一不是很重要的变量。同样的也可以进行模型筛选，这个之后讲到

但是实际上，舍去一些特征变量可能会对预测产生更多的影响。

所以使用第二个方法，引入正则化

我们会保留所有的特征变量，但是减少量级或者参数\theta_j 的大小

代价函数（正则化）

上面的图像中，第二个就是过拟合，因为使用了过多的变量来绘制曲线

上面这个函数是我们的优化目标，优化问题

我们给这个函数加上一个惩罚机制，设置\theta_3 和 \theta_4 的系数非常大

这样一来得到的特征系数\theta_3和\theta_4的值都会非常小，甚至接近于0，从而使得拟合方程变成了一个二次函数加上了一些非常小的项

这样一来其实是弱化了部分特征对于拟合曲线的影响，但是这个方法并没有减少特征的数量

上面的这个例子就是使用了正则化的思想。

如果给这些个参数都加上惩罚项，这样就相当于尽量去简化这个假设模型，如果得到这些参数都接近于0的时候

事实证明，这些参数的数值越小，我们得到的函数就会越平滑，也就越简单，也更不容易出现过拟合的问题

---

但其实，我们并不知道具体上需要减小那个特征变量的系数值，这就相当于一个盒子

在每一项上都加上正则化，但是除了\theta_0，因为这是约定俗成的，在实践中这个其实是一样的

上面公式中涉及到的 \lambda 是正则化系数，作用是控制两个不同目标之间的取舍

第一个目标于目标函数的第一项有关，就是更好的拟合数据

第二个目标是我们要保持参数尽量地小 ，与正则化的目标一样

如果\lambda（惩罚参数）设置的过大，就会导致所有的特征参数都会变得很小，甚至接近于0，也就到达了欠拟合

所以我们需要合适的选择\lambda的大小

最后写一下正则化之后的公式：

$$J(\theta )=\frac{1}{2m}[\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2+\lambda \sum _{i=1}^m{{\theta }_j}^2]$$

后续进行迭代的时候，就是上面这个函数对\theta_j进行求偏导

线性回归的正则化

上面是我们之前用到的梯度下降的算法去最小化最初的代价函数

在我们对上面这个算法进行修改的时候，我们需要对\theta_0进行特殊对待

需要注意的是上面图片中的公式，指的是进行求偏导之后

图片中第一个公式是对\theta_0求偏导之后的

第二个公式是对\theta_j求偏导之后的（包含正则化）

针对于对\theta_j求偏导之后的公式表示：

$$\begin{array}{}\text{(1)}& {\theta }_j:={\theta }_j=\alpha [\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda }{m}{\theta }_j]\end{array}$$

而对上面这个方程进行优化化简之后得到的方程为：

$$\begin{array}{}\text{(2)}& \theta :=(1-\alpha \frac{\lambda }{m}){\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}\end{array}$$

其中：

$$(1-\alpha \frac{\lambda }{m}){\theta }_j$$

的系数是很有意思的

贡献者

王海平

文件历史

最后编辑于 大约 1 个月前查看完整历史

a137c-vault backup: 2024-12-17 08:43:57