字数

904 字

阅读时间

4 分钟

微分方程的一些概念

一阶微分方程

一阶微分方程是指只有一阶导数或微分的微分方程。

注：阶数是微分方程中含有的导数或微分的最高阶数,如 $y^{\prime \prime }+xy=y\sin x$ 就是二阶微分方程了。

线性

形如

$$y^{\prime }+p(x)y+q(x)=0$$

指的是微分方程简化之后的每一项关于 $y$、 $y^{\prime }$ 的指数为 $1$.

注：这里仅仅是对于 $y$ 本身来说，对 $x$ 没限制，其中对于 $p(x)$ 和 $q(x)$ 并不做限制。形式如 $(y^{\prime }{)}^2+p(x)y+q(x)=0$，$y^{\prime }+p(x)y^2+q(x)=0$ 等形式的就不再是线性方程。

齐次

常数项（即不含有未知数的项为 $0$），称为齐次线性方程。

齐次微分方程

形如

$$y^{\prime }=f(\frac{y}{x})$$

换元后能为可分离变量方程的一类微分方程，其中 $f$ 是已知的连续方程。

一阶线性微分方程

二阶常系数线性微分方程

形如：

$$y^{\prime \prime }+p{y}^{\prime }+qy=f(x)$$

的微分方程，其中 $p$ 和 $q$ 是实常数。

解的结构

IMPORTANT

非齐次解的线性组合仍是非齐次的解，只要系数相加等于 1

IMPORTANT

非齐次解的线性组合为齐次的解，只要组合系数相加为 0

求解

主要分为以下几类：

1.一阶微分方程的的求解

2.二阶可降阶微分方程的求解

3.高阶常系数线性微分方程的求解

一阶微分方程的求解

可分离变量微分方程

首先是可分离变量的微分方程。

一般形式： $\frac{dy}{dx}=f(x)g(x)$

解法：合并同类项，然后积分。

齐次微分方程

一般形式： $\frac{dy}{dx}=f\left(\frac{y}{x}\right)$

一般不会直接得到这个形式的题目，基本上都需要化简之后得到这个形式。

求解：

令 $u=\frac{y}{x}$ ，有： $\frac{dy}{dx}=\frac{d(xu)}{dx}=u+x\frac{du}{dx}$

代入原方程，再合并同类项，然后积分。

一阶线性微分方程

一般形式： $\frac{dy}{dx}+P(x)y=Q(x)$

一阶齐次线性微分方程：

若 $Q(x)\equiv 0$ ，则通解为：

$$y=C{e}^{-\int P(x)dx}$$

一阶非齐次线性微分方程

若 $Q(x)\ne 0$ ，则通解为：

$$y=C{e}^{-\int P(x)dx}[\int Q(x)e^{\int P(x)dx}dx+C]$$

二阶微分方程

二阶齐次线性微分方程

一般形式：

$$\frac{d^2(y)}{d{x}^2}+P(x)\frac{dy}{dx}+Q(x)=0$$

通解：

$$y=C_1{y}_1(x)+C_2{y}_2(x)(C_1,C_2\in R)$$

其中的 $y_1(x),y_2(x)$ 为该方程的特解，其线性无关，也就是： $\frac{y_2(x)}{y_1(x)}\ne C$

二阶常系数齐次线性微分方程

一般形式：

$$\frac{d^2(y)}{d(x{)}^2}+p\frac{dy}{dx}+q=0(y^{\prime \prime }+p{y}^{\prime }+qy=f(x))$$

通解：

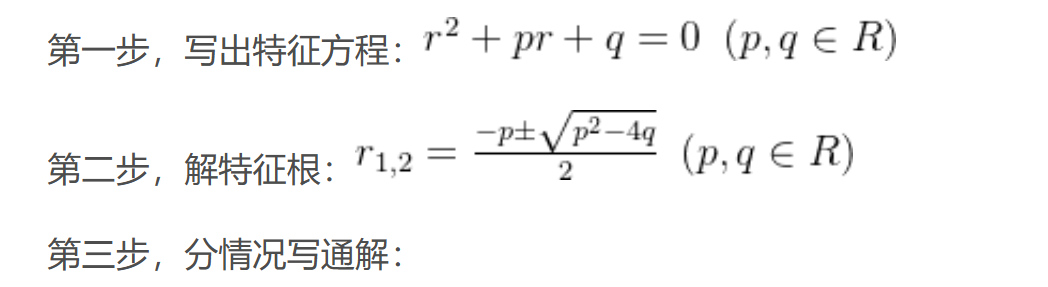
二阶常系数非齐次线性微分方程

一般形式：

$$y^{\prime \prime }+p{y}^{\prime }+qy=f(x)$$

非齐次通解 = 齐次通解 + 非齐次特解

齐次通解就是上面哪几个解，注意其个别的形式。

关键是非齐次特解：

二阶可降解微分方程

这个只有两种：

不含有 $y$ 的

在 $y^{\prime \prime }=f(x,y^{\prime })$ 中，不含有 y。

要设 $y^{\prime }=p$ ，则 $y^{\prime \prime }=p^{\prime }$

可以得到 $p^{\prime }=f(x,p)$

不含 $x$ 的

在 $y^{\prime \prime }=f(y,y^{\prime })$ ，中不含有 $x$ 的。

令 $y^{\prime }=p$ ，则 $y^{\prime \prime }=\frac{dp}{dx}=\frac{dp}{dy}\cdot \frac{dy}{dx}=p\cdot \frac{dp}{dy}$

所以，可以得到：

$$p\cdot \frac{dp}{dy}=f(y,p)$$

贡献者

王海平

文件历史

最后编辑于 14 天前查看完整历史

74726-vault backup: 2025-04-10 21:51:48