一、快速抓大头
抓大头直接得到结果:
二、
例题:
这个函数的图像如下:
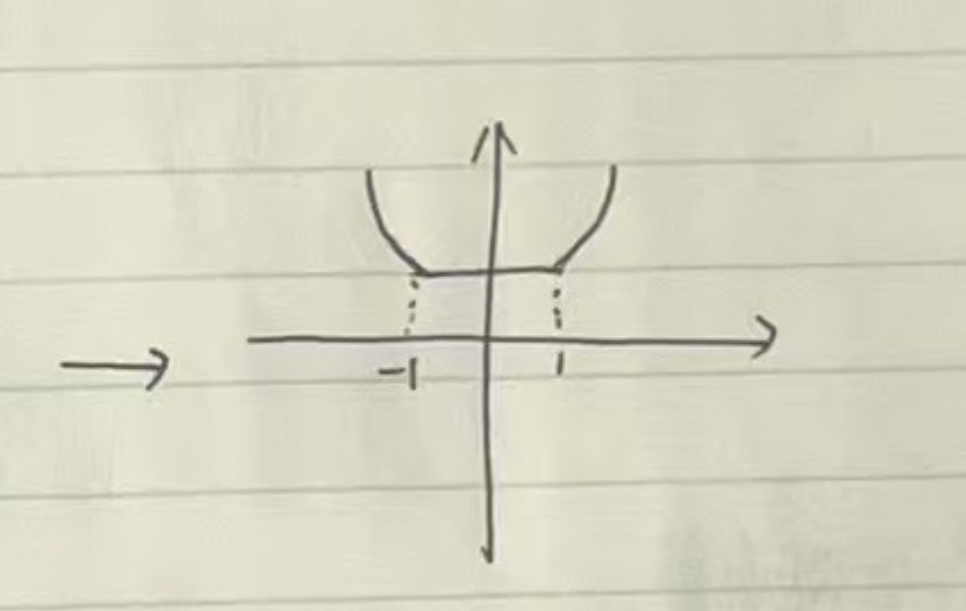
可以很轻松的得到
三、指数相乘三角函数的快速求积分
这个是对于指数相乘三角函数的快速求积分的方法
需要注意的是,核心是计算这个行列式。
四、
需要记忆这个函数的图像。
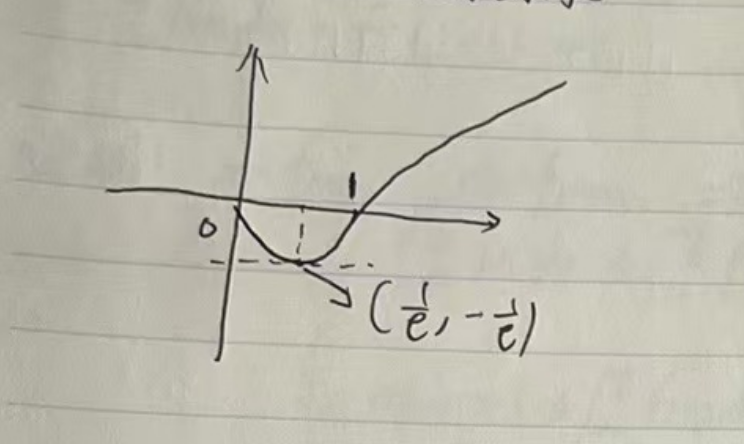
五、
记忆
的有关性质。
1、
2、
3、
这个公式的推导来自于基本积分公式:
4、
等价无穷小,这个有时候用的挺多的
一般只用到前两项,如果还有必要,做题遇到再说,因为这个函数的导数不是很好求,不过依然可以用泰勒展开求解。
六、关于
1、
2、
3、
4、
七、导数与原式同时出现
如果
第一个,考虑拉格朗日中值定理
第二个,考虑积分
八、常见函数的极限
例题:
这里需要分左右极限来处理。
九、变上限积分的无穷小
例题:
根据上面的公式,得到原式是
十、三步走和四步走
对于
可以得到:
核心在于将
对于
可以得到:
关键是在于要学会对
十一、三角恒等变换相关公式
积化和差以及和差化积公式
记忆口诀: 正加正,正在前, 余加余,余并肩。 正减正,余在前, 余减余,负正弦。
积化和差公式:
记忆口诀: 积化和差得和差, 余弦在后要相加; 异名函数取正弦, 正弦相乘取负号。
和差角公式
六边形关系
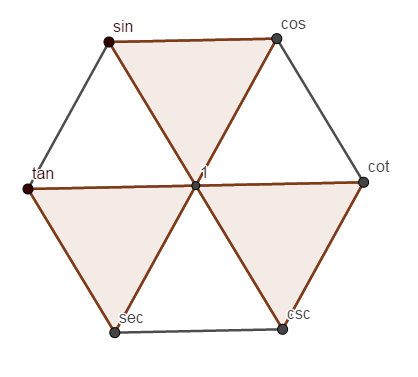
其中有三组关系:
- 边上的三角函数两边相乘等于中间
- 染了色的三角形上面两个三角函数的平方和等于下面的
- 相对的三角函数是倒数关系
二倍角公式
三倍角公式
半角公式
注意,具体需要符号看象限
降幂公式
辅助角公式
其中,
点鞭炮公式
万能公式
辅助记忆图:
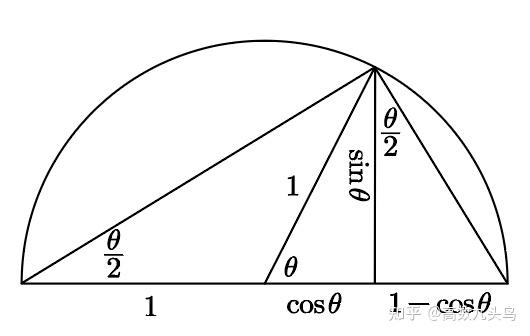
十二、切线方程
过
若过P另有曲线C的切线,切点为
十三、曲率与曲率半径
曲率,主要是用到了与导数相关的知识。
曲率:
曲率半径:
十四、曲线渐近线问题
曲线的斜渐近线
上面公式中的
曲线的水平渐近线
当
曲线的垂直渐近线
十五、欧拉公式
十六、泰勒公式的一些应用
首当其冲的就是求极限
这个就不多讲了,不过需要注意的是,一般上来讲,是
其次,就是泰勒公式与高阶导数之间的关系
这里不再赘述。
这里主要是说明泰勒公式在求和方面的应用。(或许未来会整理到一个单独的文件中。)
注意到常见的泰勒展开式前面是有系数的。
也就是说,当涉及到"系数"相加的情况,可以考虑泰勒公式。
例如下面这两个例子:
这里主要用到了
令
另外一个例子:
这个是用到了
当
以此类推,可能会有
十七、一些积分相关的东西
基本积分公式
下面补充积分:
形如
核心要义就是令分子 = A 分母+B 分母的导数
例如:
令
可有得到:
IMPORTANT
这里暂定,有些许问题,后续再处理。
十八、圆
圆的标准方程:
在平面直角坐标系内,以
圆的一般方程,也是在平面直角坐标系内。
其中,
圆心:
半径:
注意,若
参数方程:
圆心为
极坐标方程:
圆的半径为
圆心在极点处时候:

极坐标方程为:
圆心在极轴上的圆,半径为

极坐标方程表示为:
过极点的圆:
圆心为

极坐标方程为:
十九、四种常用曲线
经常用于定积分求面积以及二重积分求体积。
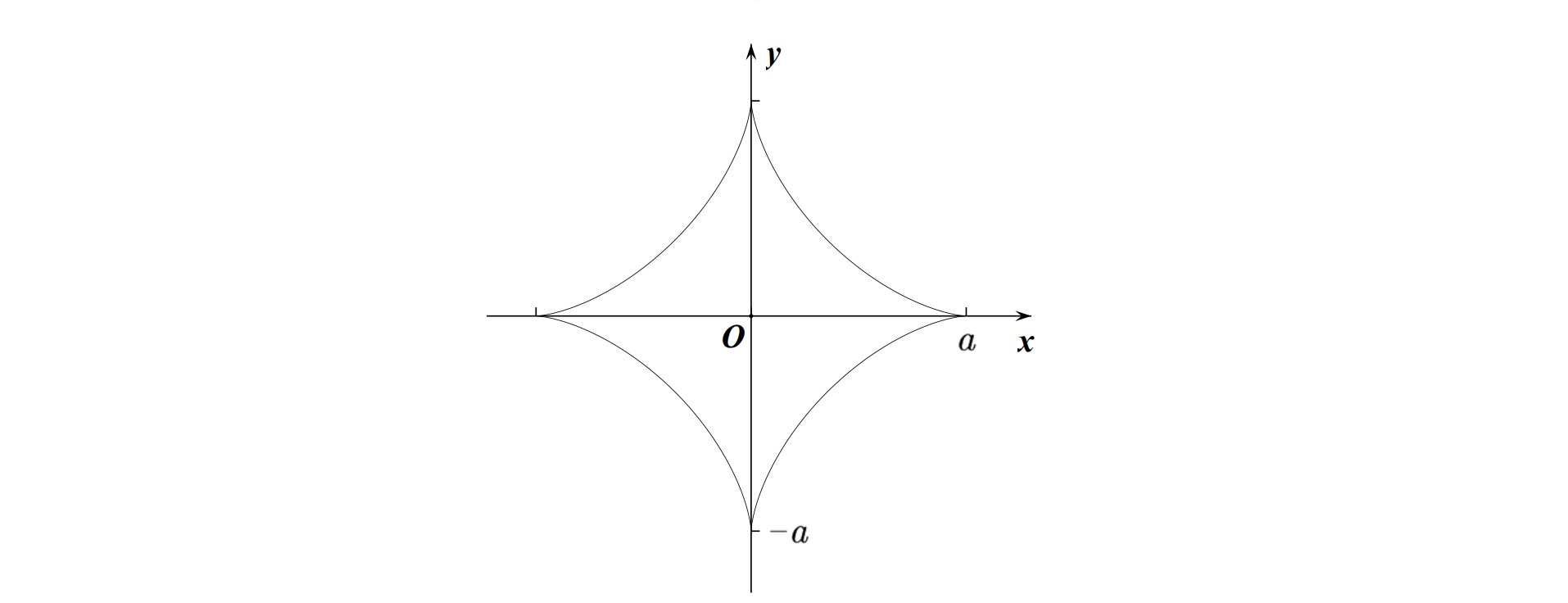
星形线
基本方程:
参数方程:
图像:
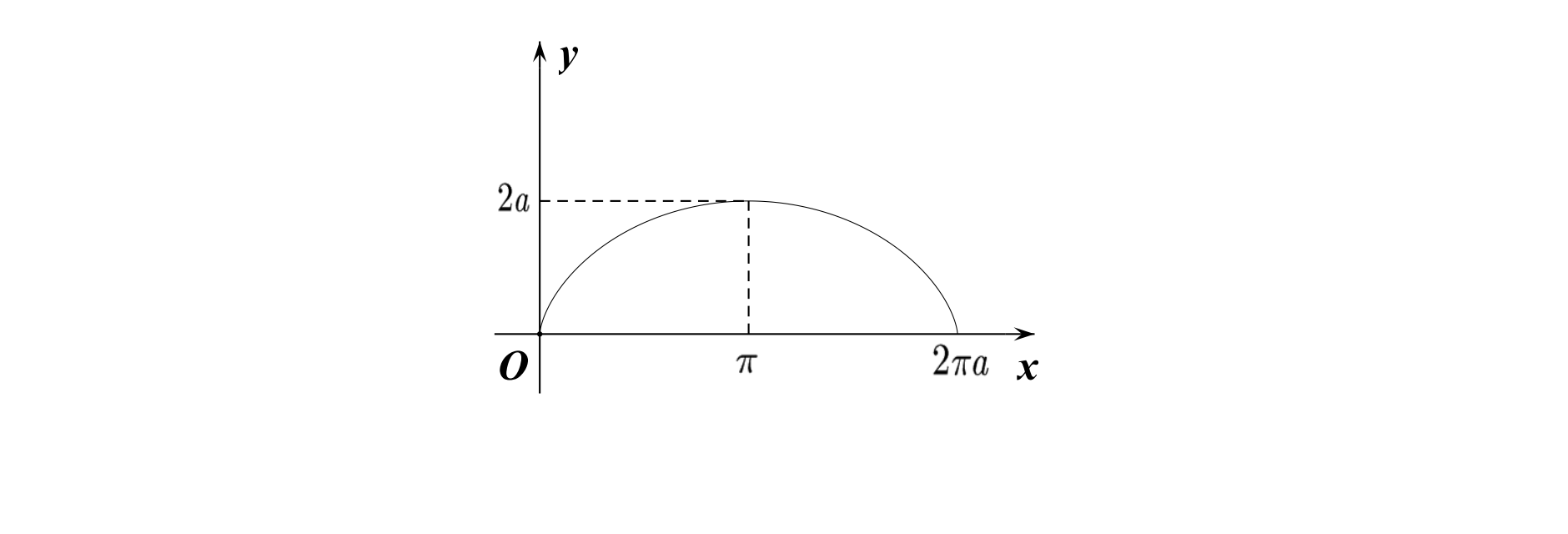
摆线
参数方程:
图像:
心形线
基本方程:
极坐标方程:
图像:
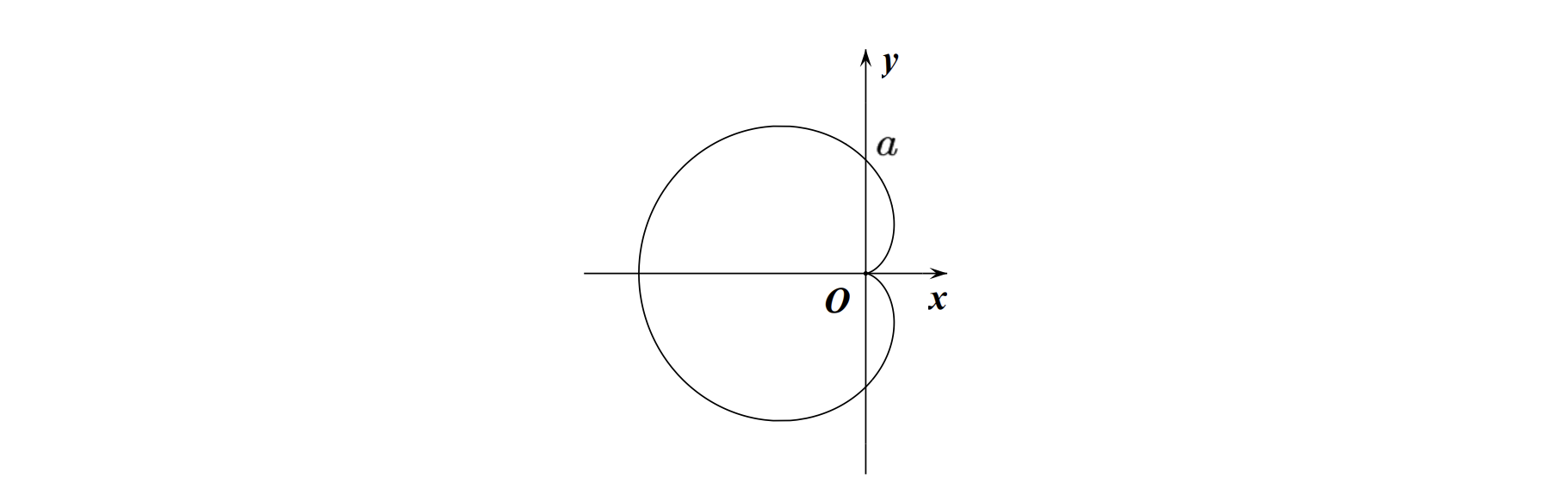
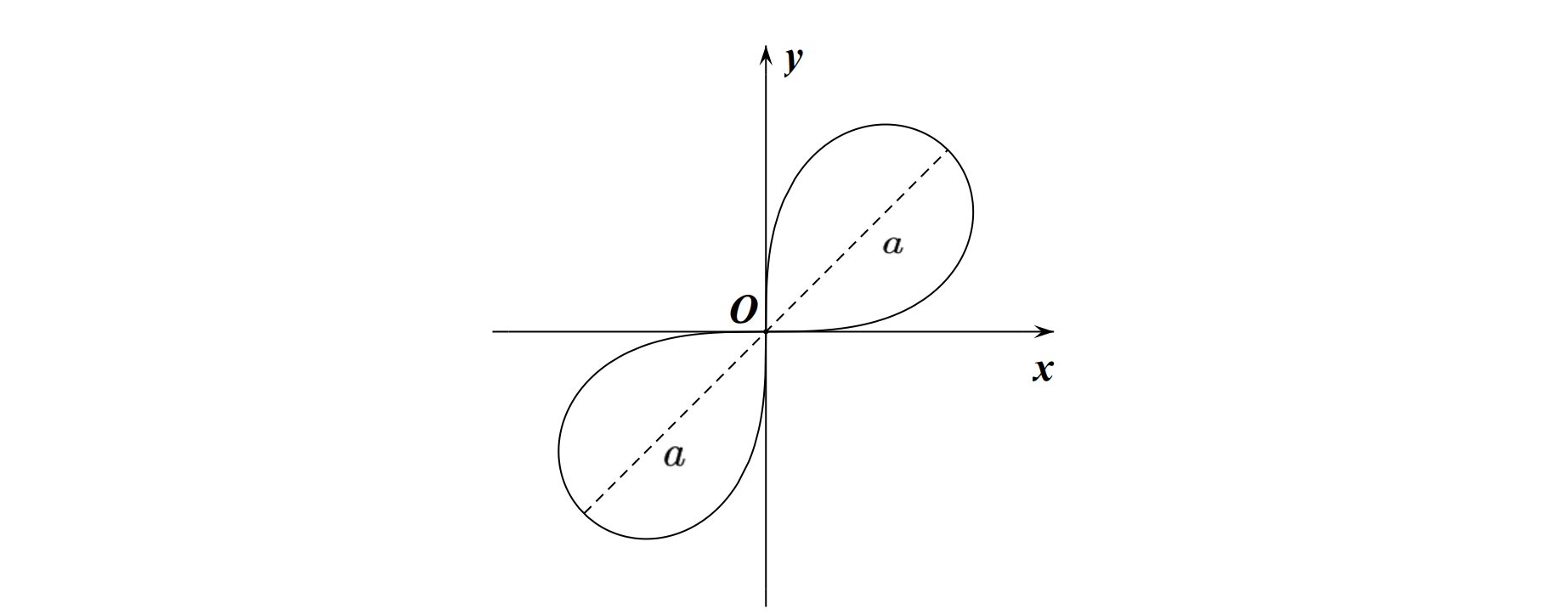
伯努利双纽线
双纽线有两个,一个关于
一般方程:
极坐标方程:
图像:

原点对称双纽线
一般方程:
极坐标方程:
图像:
二十、定积分求体积
些许题目的可以使用传统的求体积的方法:
贴近 x 轴 y 轴求体积
绕 x 轴旋转一周:
绕 y 轴旋转一周:
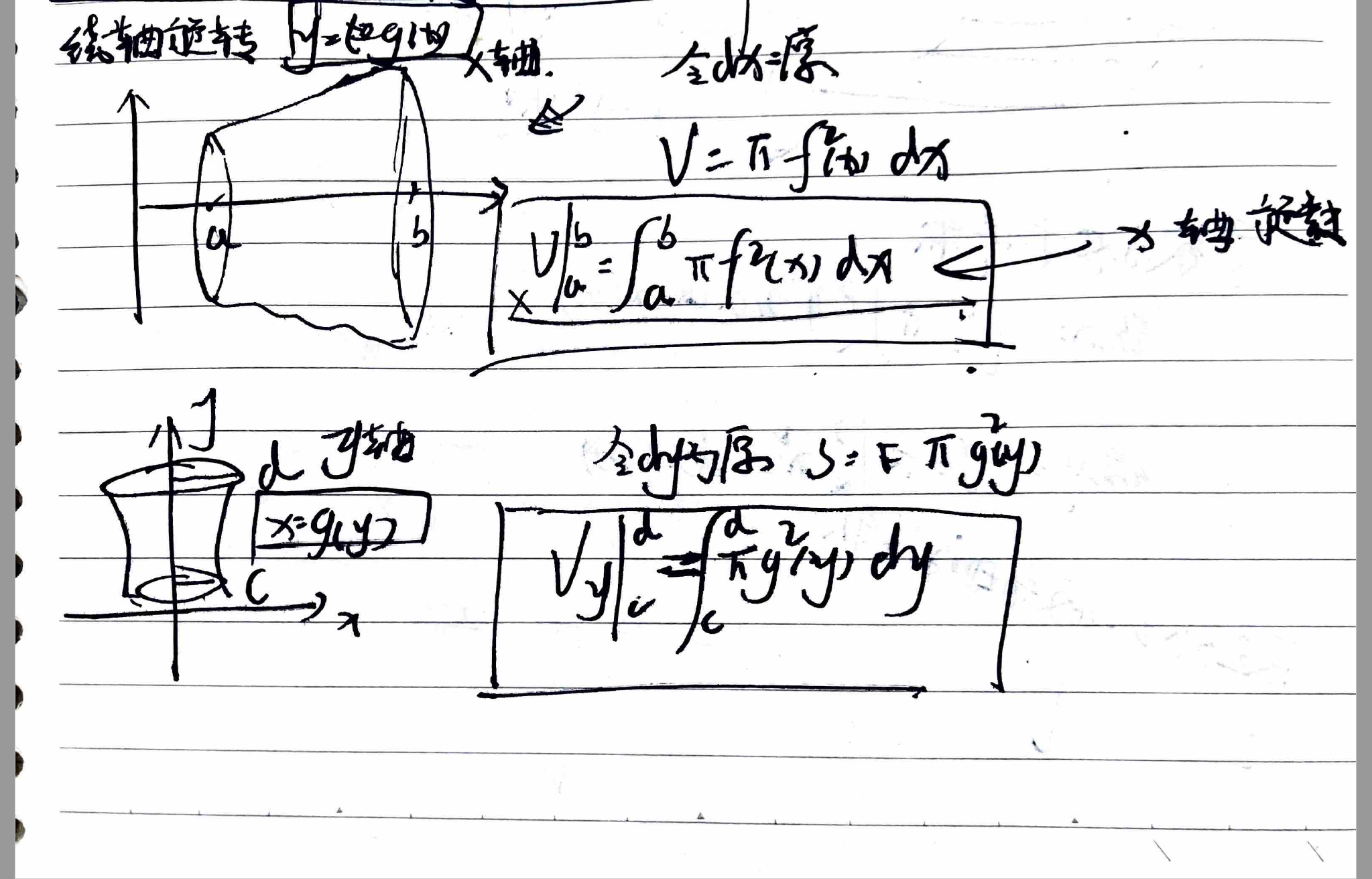
上面的公式适用于旋转体与 x 轴或 y 轴相近的情况,如果出现不相接触的情况用下面这个公式:
不贴近 x 轴 y 轴求体积
绕 y 轴:
绕 x 轴:
IMPORTANT
注意,上面绕 x 轴公式中的
参数方程求体积
直接上方程
绕 x 轴:
绕 y 轴:
极坐标绕极轴的体积
除极坐标的通用方法
利用二重积分求解定积分体积问题。
任意图形绕任意轴旋转一周的体积,有公式:
其中
直线距离公式:设直线方程为
用语言描述就是,将这个点代入到这个方程中,然后除以方程系数平方和的开根号。
这么说不太好理解,来个例题:
求
根据上面的方法,可以直接列公式:
上面就是利用二重积分求解体积。
不过需要注意的是,上面这个限制范围的
求
依然是直接列公式:
二十一、柯西积分不等式
若
二十二、定积分与常数不等式
二十三、奇函数积分与偶函数积分
二十四、基本不等式
对于正实数
按照顺序得到的结果是:
调和 < 几何 < 算术 < 平方
被称为调几算方
N 元均值不等式
对于任意的正整数
二十五、拉格朗日乘数法求解多元函数极值点

 王海平
王海平